Hi there!
I’m an electrical engineering student trying my hands on optimisation, and would like to solve a system with quadratic combinations of data contained in a vector b, as seen below.
![]()
I really tried finding my answers in the book of Boyd and Vandenberghe, and other littereture on the topic, but I am finding it hard to sort out the relevant information in all the new stuff I am reading. Therefore I thought I’d try my luck here.
For solving this problem i i found a rank minimization technique in here:
In "M.Fazel, H.Hindi, and S.Boyd,“Rank minimization and applications in system theory,” presented at the Amer. Contr. Conf. Boston, MA, USA, Jun. 2004. , and uses this to encourage low-rank solution, since I have relaxed my problem with a semidefinite relaxation.
My optimization problem then looks as follows:
![]()
subject to
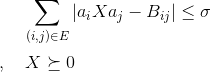
The idea is to be able to choose specific quadratic combinations of the vector b with a “selector matrix” E.
Se code below (implemented in MATLAB)
cvx_begin quiet
variable X(sysdata.N,sysdata.N) hermitian semidefinite
minimize( trace((X_last+sysdata.delta*I)^(-1)*X) )
subject to
for i = 1:sysdata.M
for j = 1:sysdata.M
if sysdata.E(i,j) == 1
Qij = A(j,:)'*A(i,:);
abs(trace(Qij*X)-B(i,j)) <= sig;
end
end
end
X == hermitian_semidefinite(sysdata.N)
cvx_end
My questions:
Program is running rather slowly, is there any way to speed it up?
How is my problem convex or what ensures the convexity?
Thank you in advance
Rasmus