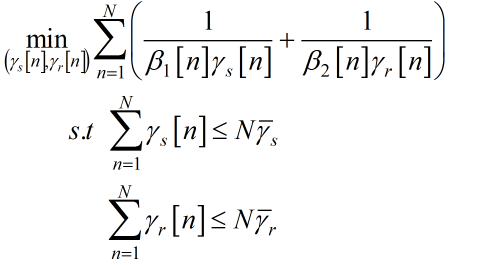Hi, i want to solve the simple convex problem as below ,
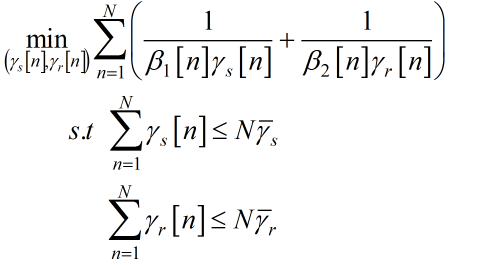
where, beta _1 is monotonically decreasing n, beta _2 is monotonically increasing n, and all the variables are nonnegative.
when I use mosek solver, the value of gamma _s are obtained as following,
using sdpt3,the the value of gamma _s are obtained as following,
the matlab code is given by
function [ Snr_PS,Snr_PR ] = CvxFixedTrajectory(Belta1,Belta2,Snr_PS_av,Snr_PR_av)
global N;
cvx_solver mosek
% cvx_solver sdpt3
cvx_begin
variable Snr_PS(N) nonnegative
variable Snr_PR(N) nonnegative
expression SumBelta1(N)
expression SumBelta2(N)
for i=1:N
SumBelta1(i)=inv_pos(Belta1(i)*Snr_PS(i));
end
for i=1:N
SumBelta2(i)=inv_pos(Belta2(i)*Snr_PR(i));
end
minimize sum(SumBelta1+SumBelta2)
subject to
sum(Snr_PS)<=N*Snr_PS_av;
sum(Snr_PR)<=N*Snr_PR_av;
cvx_end
What are the reported solver and CVX statuses? What are the cvx_optval values? How much do they differ?
Hi, Mrak,
When I use mosek solver , the CVX report that
Status: Solved
Optimal value (cvx_optval): +1.0238
The gamma_s =
41497408134.8427
41373889096.3778
41251844355.7951
41131982910.6007
41014907659.0074
40901114464.3990
40790994361.9145
40684838195.1278
40582842121.2886
40485115029.5839
40391687387.4095
40302520156.9958
40217514151.2293
40136520210.7761
40059349162.8923
39985780912.7997
39915573791.3414
39848472966.9939
39784217593.9545
39722547929.8381
39663210643.2286
39605963116.5146
39550577567.6784
39496843034.5281
39444567431.7250
39393578305.7568
39343723447.2670
39294870087.4556
39246904499.9522
39199730868.1861
39153269961.0223
39107457674.1947
39062243572.3918
39017588984.5042
38973465955.6010
38929855419.7290
38886745892.3162
38844132249.8766
38802014246.3878
38760395900.2142
38719284346.4525
38678688766.8805
38638620218.4890
38599090430.2491
38560111887.1642
38521696807.5367
38483857399.8370
38446604990.6204
38409950394.1603
38373903163.9704
38338472055.1329
38303664427.5587
38269486429.2648
38235943171.0010
38203038294.6662
38170774203.7951
38139152325.7321
38108172690.0578
38077834209.5619
38048134962.7066
The gamma_r =
38032666120.5372
38061911800.8787
38091791327.8255
38122307251.2737
38153461388.2814
38185254579.9309
38217686468.4727
38250755827.4665
38284460414.9069
38318796743.3420
38353760582.6742
38389346483.0350
38425548288.8257
38462359139.9057
38499771295.4954
38537776967.6351
38576367881.3183
38615536276.6100
38655274668.1756
38695576935.6002
38736438353.2737
38777856472.3649
38819832150.9356
38862369936.5296
38905479371.3970
38949175941.1669
38993482605.8876
39038430624.4285
39084061273.1057
39130427203.4446
39177593924.6586
39225641264.0614
39274664743.6206
39324776815.3553
39376107908.2064
39428807090.8346
39483042505.9255
39539000773.8013
39596886674.8971
39656921309.1690
39719339512.8546
39784386686.5552
39852314774.8614
39923376423.8772
39997819009.7966
40075877324.3492
40157765438.8781
40243667893.1645
40333730396.2750
40428049713.5189
40526664525.9614
40629545007.7703
40736583938.3016
40847587940.8070
40962269931.7120
41080242344.6079
41201013267.4613
41323983105.9070
41448445847.8422
41573592308.5433
As for sdpt3 solver, the CVX report that
Status: Solved
Optimal value (cvx_optval): +1.0147
The gamma_s =
39188413718.6215
39357681180.4697
39519970536.4526
39674632259.3342
39821086421.4164
39958815746.0051
40087360435.0307
40206314952.8485
40315326764.9038
40414096934.8761
40502382119.0857
40579997436.1484
40646819865.1865
40702791170.8351
40747920274.9461
40782284560.8643
40806029565.4332
40819367361.6985
40822573161.9681
40815980395.8622
40799974539.5717
40774985693.7220
40741480374.7900
40699952947.5700
40650916615.7923
40594894763.9647
40532412727.7280
40463990204.0276
40390134573.8494
40311335381.2296
40228059752.4689
40140749272.3202
40049817664.0972
39955649907.0458
39858602016.3455
39759001817.9366
39657150344.4110
39553323577.9469
39447774591.8551
39340735854.4362
39232421208.8481
39123028053.3135
39012738890.9253
38901722752.8324
38790136105.2649
38678123388.9618
38565817312.2804
38453338686.8656
38340796196.2322
38228285991.3720
38115891351.2953
38003682422.8504
37891716336.0840
37780037544.8634
37668678701.1039
37557662089.7945
37447001615.2245
37336705426.6683
37226779106.6667
37117229623.0676;
gamma_r=37208630358.5899
37317854341.9323
37427503575.3642
37537572781.7899
37648053837.9916
37758932651.6314
37870186639.8044
37981782796.2468
38093676362.9925
38205810017.0737
38318113463.1233
38430503440.1793
38542883817.6499
38655146059.1724
38767169381.0900
38878821128.5447
38989956605.2839
39100418878.9462
39210038079.2175
39318630373.0260
39425996487.8016
39531919956.5319
39636165105.6755
39738474751.6219
39838568010.6215
39936138196.6647
40030850895.4594
40122342790.0010
40210220887.4288
40294062717.2818
40373417565.6745
40447808637.8010
40516736571.9789
40579684058.0019
40636121582.5166
40685514319.1301
40727329793.7879
40761046513.0872
40786162737.2896
40802205563.6653
40808739884.5143
40805376640.3918
40791780471.7957
40767675946.9938
40732852699.4262
40687168734.5967
40630552332.0944
40563002110.7960
40484585875.4507
40395438116.2762
40295756864.9008
40185800223.1396
40065883218.3867
39936375524.7262
39797700562.5718
39650336264.6763
39494818027.0886
39331743360.1759
39161778385.3295
38985665274.6133;
Two of them are all solved, and the optimal value are nearly same. Actually, the above minimization problem is convex ,thus must have one global solution, Also , the two solution about gamma_s and gamma_r are not the results what are expected, from the KKT, it is not difficult to verified that the gamma_s should monotonically increasing with N and gamma_r should monotonically decreasing with N, respectively .
I hope this not trouble you too much !
I don’t know the details of what you’ve done, but your gamma_s and gamma_r values seem rather large at approximately 4e10. I don’t know whether there might be some numerical stability problems associated with that/. Can you rescale your inputs so that optimal values are closer to 1?
Hi,Mark. thanks for your reply ,i have tried use simple case, the using different CVX solvers, the results are same and work well. just like you say, this problem may be associated with numerical stability.
At last , much appreciated to you .