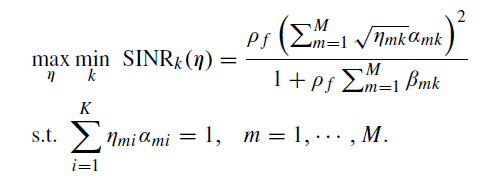
Hey guys, Im trying to solve that above problem with cvx but I getting this error all time. I’ve tried to put pow_abs or pow_p instead but it does not work, would someone know how to fix it? thxs
Error:
Disciplined convex programming error:
Illegal operation: {concave} .^ {2}
(Consider POW_P, POW_POS, or POW_ABS instead.)
Error in .^ (line 55)
z = pow_cvx( x, y, ‘power’ );
Error in p_tac (line 127)
S=p(1).* PS.^2;
This is my code:
M=8; %Puntos de acceso
K=4; %Usuarios
v_shad=8 ;%Varianza de Shadowing
p=ones(1,M); %potencia total maxima
dx=2; %desnsidad de la malla en el eje x (km)
dy=2; %desnsidad de la malla en el eje y (km)
n_ptos=10;
x=linspace(0,dx,n_ptos);
y=linspace(0,dx,n_ptos);
[X,Y] = meshgrid(x,y);
%% Posicionamiento de los usuarios y de las estaciones base(APs)
users=randi([1 n_ptos],2,K); %posicion de cada usuario dentro de la malla(X,Y)
ptos_acceso=randi([1 n_ptos],2,M); %posicion de cada PAs dentro de la malla(X,Y)
%% Canales de cada usuario a cada APs
%Calculamos la distancia entre cada uno de los APs a todos los usuarios
dm=zeros(M,K);
for i=1:M
for j=1:K
d_p=ptos_acceso(:,i);
c_p_a=[ X(1,d_p(1)) Y(d_p(2),1)];
d_u=users(:,j);
c_user=[ X(1,d_u(1)) Y(d_u(2),1)];
d=c_user-c_p_a;
dm(i,j)=norm(d);
if dm(i,j)==0
dm(i,j)=0.01;
end
end
end
Xm=randn(M,K)*v_shad;
Bm=-136-35*log10(dm)+Xm; %Path loss (dB)
bm=10.^(Bm./10);
hm=sqrt(1/2)*(randn(M,K) + 1i*randn(M,K));% CN(0,1)
gm=sqrt(bm).*hm; %canales complejos
%% Señal enviada
%cada APs envia un BPSK[-1 1]
s=randi([-1,1],M,K); %cambiarlo
xm=zeros(M,1);
%n_s=zeros(M,K); % Parametro a optimizar
n_s=[0.2 0.3 0.1 0.4
0.1 0.1 0.7 0.1
0.2 0.3 0.1 0.4
0.2 0.3 0.1 0.4
0.2 0.3 0.1 0.4
0.2 0.3 0.1 0.4
0.2 0.3 0.1 0.4
0.2 0.3 0.1 0.4];
for i=1:M
xk=zeros(1,K);
for j=1:K
xk(1,K)=n_s(M,K)*conj(gm(M,K))*s(M,K);
end
xm(M,1)=sqrt(p(M))*sum(xk);
end
%% Calculo de la SNR(Optimizacion) FULL POWER TRANSMISION
am=abs(gm).^2;
S=zeros(1,K);
I=zeros(1,K);
%SNR=zeros(1,K);
PS=zeros(M,K);
PI=zeros(M,K);
tl=0;
tu=10000;
t=1/2*(tl+tu);
%m=1:lenght(M)
%PI_prueba=sqrt(n_s).*am.*bm
% for k=1:K
%
% for m=1:M
%
% % PS(m,k)=sqrt(n_s(m,k))*am(m,k);
%
% for i=1:K
% %PI(i,k)=sqrt(n_s(m,i))*am(m,i)*bm(m,k);
% %PI(i,k)=1;
% end
% end
I=ones(1,K)+p(1).*sum(bm);
cvx_begin
variable n_sa(M,K) nonnegative
expression SNR(1,K)
% minimize(SNR)
maximize(n_sa)
PS=diag(sqrt(n_sa')*am)';
S=p(1).* PS.^2;
SNR=S./I;
subject to
diag(n_sa*am') == ones(M,1) ;
cvx_end