When i use cv to solve this optimization problem,something wrong,can you help me

1 
indent preformatted text by 4 spaces
Nt = 10;
Nrf = 4;
h = rand(Nt,1)+1i*rand(Nt,1);
f1 = rand(Nrf,1)+1i*rand(Nrf,1);
F1 = rand(Nt,Nrf)+1i*rand(Nt,Nrf);
cvx_begin 
variable F(Nt,Nrf)  complex
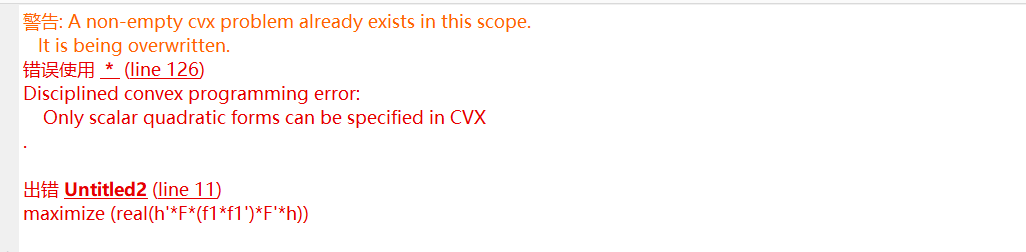
minimize (real(h'*F*(f1*f1')*F'*h))
subject to
    norm(F,'fro')<=1
cvx_end

微信截图_20220508111621
微信截图_202205081116211026×252 7.28 KB

3

the hessisan matrix of the objective function is 2(\mathbf{f}\mathbf{f}^H )\otimes(\mathbf{h}\mathbf{h}^H) is semidefinite, thus the objective function is a convex function

4

sorry, it is convex. so you can only minimize it in CVX.

5

微信截图_20220508135455
微信截图_202205081354551111×324 9.14 KB

yes, it’s convex, but the same error occurs.

6

minimize(norm(h'*F*f1,'fro'))

7

thanks you very much, i have got it

8

The norm(,‘fro’) trick works here, and is especially useful when there is trace(matrix). It is a good formulation here.

But in this case, it would also be sufficient to apply “grouping” via parentheses, which ensure that a vector transpose is multiplied by itself, which is allowed by CVX as constituting a convex expression because it is a convex quadratic.
minimize((f1'*F'*h)'*(f1'*F'*h))
as a side bonus, the real is not necessary when doing it this way.

or

x = f1'*F'*h;
minimize(x'*x)
9

ok, thank you very much, i have got it