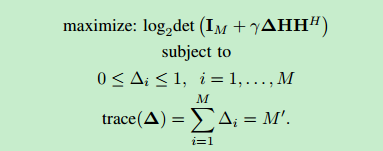What should I do to deal with 'det'?

1

Here is the problem.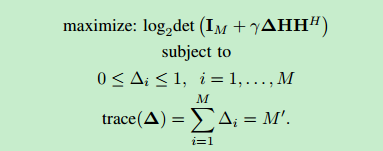

And my code is below。

Ns = 4;
Nr = 16;
Lr = 5;
H = randn(Nr,Ns);
SNR_dB=10;
SNR_linear=10.^(SNR_dB/10.);
I = eye(Nr);

lower_bound = zeros(Nr,1);
upper_bound = ones(Nr,1);

cvx_begin
variable x(Nr)
C = I+SNR_lineardiag(x) H*(H’);
maximize( log_det(real©) )
subject to
lower_bound <= x <= upper_bound;
sum(x) == Lr;
cvx_end

Matlab told me that
CVX Warning:
Models involving “log_det”……
Error using det_rootn
Error in log_det

How can I figure it out? Thank you very much.

2

I ran your code as is. It successfully executed to optimal solution for several random instances, using both sedumi and sdpt3, although there were many “Matrix is close to singular or badly scaled” warning messages under sdpt3.

Because of the use of log_det, I received the standard CVX warning

CVX Warning:
Models involving “log_det” or other functions in the log, exp, and entropy
family are solved using an experimental successive approximation method.
This method is slower and less reliable than the method CVX employs for
other models. Please see the section of the user’s guide entitled
The successive approximation method
for more details about the approach, and for instructions on how to
suppress this warning message in the future.

But this is not an error message. And indeed the optimization problem was successfully solved.

3

Dear Sheng Chi,

I am trying to solve the exact same problem, but I am getting an ‘x’ with same equal entries, regardless the channel matrix.

Here is my code:
cvx_begin
variable x(Mr)
maximize( log_det( eye(Mr) + EbN0diag(x)(Hfull*Hfull’))/(log(2)) )
subject to
zeros(Mr,1) <= x <= ones(Mr,1)
x <= ones(Mr,1)
sum(x) == L;
cvx_end

I know it has been a while, but I was wondering if you were able to solve your problem…