The solution of cvx is always 0, and each run is exactly the same, and the generated power P does not meet the constraints.
Show your complete output, not just part of it. and maybe post your code out in markdown format, so someone can reproduce your problem.
function [Q_,P_] = CVX_theta_Optimal(M,P_max,K,Z,v,q,p)
cvx_begin
cvx_quiet false;
variable Q(M+1,M+1) hermitian semidefinite
expression F(K)
expression G(K)
expression G_gradient
expression P(K)
for i=1:K
if i == 1
s_inter = 0;
G_tmp = 0;
else
for j=1:i-1
s_inter = p(j).*(trace(Z(:,:,j)*q)+ square(abs(v(:,j)))) + s_inter;
G_tmp = G_tmp + Z(:,:,j)';
end
end
G_gradient = G_tmp/log(2)*(s_inter+1);
G(i) = log(real(s_inter+1))+2*real(trace(G_gradient.'*(Q-q)))/log(2);
F(i) = -log(real(trace(Z(:,:,i)*Q)+abs(v(:,i)).^2))/log(2);
end
minimize sum(P)
subject to
diag(Q) == 1 ;
for i = 1:K
0<=P(i)<=P_max;
P(i) = real(G(i))+F(i) ;
end
cvx_end
Q_ = Q;
P_ = P ;
end
This is my code
This is the output of power；It is always one and does not satisfy the constraints.
Thank you so much for helping me take a look.
P(i) = real(G(i))+F(i) should be P(i) == real(G(i))+F(i). pls read the,cvx users’ guide.
This error is like this, P is an expression about Q, it is not a number.
function [Q_,P_] = CVX_theta_Optimal(M,P_max,K,Z,v,q,p,BER)
cvx_begin
cvx_quiet false;
variable Q(M+1,M+1) hermitian semidefinite
variable P(K)
expression F(K)
expression G(K)
expression G_gradient
expression A(K)
for i=1:K
if i == 1
s_inter = 0;
G_tmp = 0;
else
for j=1:i-1
s_inter = p(j).*(trace(Z(:,:,j)*q)+ norm((v(:,j)))) + s_inter;
G_tmp = G_tmp + Z(:,:,j)';
end
end
G_gradient = G_tmp/log(2)*(s_inter+1);
G(i) = log(real(s_inter+1))+2*real(trace(G_gradient.'*(Q-q)))/log(2);
F(i) = -log(real(trace(Z(:,:,i)*Q)+norm(v(:,i))))/log(2);
end
% expression N
%
% norm_grad = two_norm_grad(q);
% N = norm_nuc(Q)-norm(q)+2real(trace(norm_gradnorm_grad’*(Q-q)));
%
minimize sum§
subject to
for i=1:K
0<P(i)<=P_max;
end
diag(Q) == 1 ;
for i = 1:K
A(i) = 2.^((real(real(G(i))+F(i))+log(power((5.5+sqrt(1/200)*qfuncinv(BER)/log(2)),2)-1)/log(2)));
A(i)<=P(i);
end
% N = 0;
cvx_end
I change my code to this ,but this solution is very small,it not satisfy this constraint.
Follow the instructions at CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions .
function [Q_,P_] = CVX_theta_Optimal(M,P_max,K,Z,v,q,p,BER)
cvx_begin
cvx_quiet false;
variable Q(M+1,M+1) hermitian semidefinite
variable P(K)
expression F(K)
expression G(K)
for i=1:K
if i == 1
s_inter = 0;
G_tmp = 0;
else
for j=1:i-1
s_inter = p(j).(trace(Z(:,:,j)q)+ norm((v(:,j)))) + s_inter;
G_tmp = G_tmp + Z(:,:,j)’;
end
end
G_gradient = G_tmp/log(2)(s_inter+1);
G(i) = -rel_entr(1,real(s_inter+1))+2real(trace(G_gradient.’(Q-q)))/log(2);
F(i) = -(-rel_entr(1,(real(trace(Z(:,:,i)Q)+norm(v(:,i))))))/log(2);
end
% expression N
% norm_grad = two_norm_grad(q);
% N = norm_nuc(Q)-norm(q)+2real(trace(norm_gradnorm_grad’(Q-q)));
minimize P(1)+P(2)+P(3)+P(4)
subject to
for i=1:K
0<=P(i)<=P_max;
end
diag(Q) == 1 ;
for i = 1:K
P(i)-exp(log(2)(log(2.^(2+(sqrt(1/200)*qfuncinv(BER)/log(2)))-1)/log(2)+real(real(G(i))+F(i))))>=0;
end
% N = 0;
cvx_end
%Q
P
Q_ = Q;
P_ = P;
end
I change my code to this.Although the optimal value can be generated, it is still not satisfied with the constraint, and the gap is very large. Sometimes NAN also occur.Can you help me see what is the problem?
Thank you !Hope you can help me take a look at this problem.
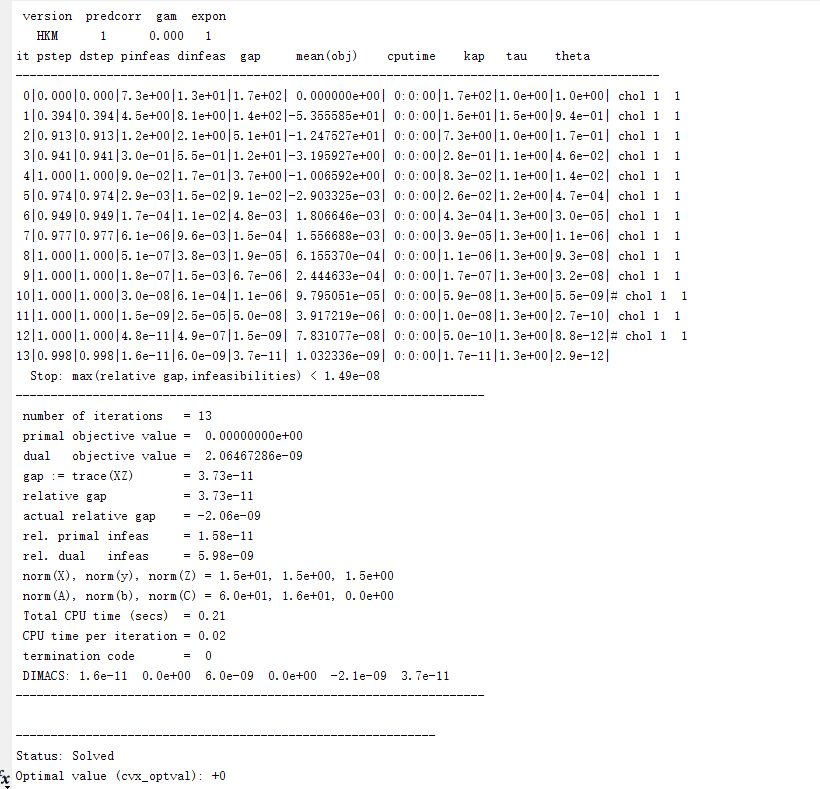
You haven’t shown us the output. We don’t even know what solution method was used. Note that constrains are not satisfied exactly, but only to within a tolerance. And CVX reported that your problem was solved inaccurately. It is possible that your input data is not well-scaled.
Sorry，This is my code and output.
function [Q_,P_] = CVX_theta_Optimal(M,P_max,K,Z,v,q,p,BER)
cvx_solver mosek
cvx_begin
cvx_quiet false;
variable Q(M+1,M+1) hermitian semidefinite
expression F(K)
expression G(K)
expression P(K)
for i=1:K
if i == 1
s_inter = 0;
G_tmp = 0;
else
s_inter = 0;
G_tmp = 0;
for j=1:i-1
s_inter = p(j).*(trace(Z(:,:,j)*q)+ sum(abs(v(:,i)).^2)) + s_inter;
G_tmp = G_tmp + Z(:,:,j).';
end
end
G_gradient = G_tmp/log(2)*(s_inter+1);
G(i) = real((s_inter+1))/log(2)+2*real(trace(G_gradient.'*(Q-q)));
F(i) = -(-rel_entr(1,(real(trace(Z(:,:,i)*Q)+sum(abs(v(:,i)).^2)))))/log(2);
end
%expression N
%norm_grad = two_norm_grad(q);
%N = norm_nuc(Q)-norm(q)+2*real(trace(norm_grad*norm_grad'*(Q-q)));
minimize sum(P)
subject to
diag(Q) == 1 ;
for i=1:K
0<=P(i)<=P_max;
end
for i=1:K
P(i)-exp(log(2)*(log(2.^(1+(sqrt(1/200)*qfuncinv(BER)/log(2)))-1)/log(2)+real(G(i)+F(i))))>=0;
end
%N = 0;
cvx_end
%Q
P
Q_ = Q;
P_ = P;
end
Successive approximation method to be employed.
Mosek will be called several times to refine the solution.
Original size: 8551 variables, 89 equality constraints
8 exponentials add 56 variables, 32 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
0/ 2 | 8.000e+00 6.868e+02 3.299e+43 | Infeasible
Status: Infeasible
Optimal value (cvx_optval): +Inf
P =
NaN
NaN
NaN
NaN
I don’t know why this problem occurs. I don’t know how to modify my code to make it run normally. Please help me, thank you!!!
Sorry，This is my code and output.
Follow the advice in the link in my previous post.
if the problem is still reported infeasible, follow the advice (except for section 1) at https://yalmip.github.io/debugginginfeasible .
Thank you very much！
Actually, as I wrote in the other thread, make sure you are using CVX 2.2 and Mosek 9.x. Otherwise you would not be getting the output with Cones | Errors … which shows the Successive approximation method was used.