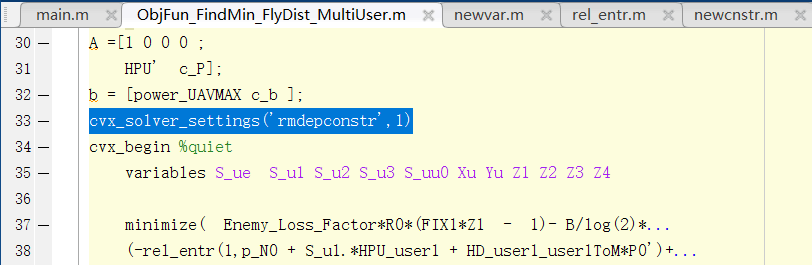
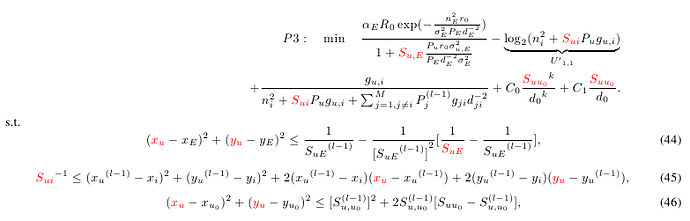The Optimization problem is convex. But sometimes CVX failed to find the optimal solution

Christ · July 3, 2019, 1:05pm

The Optimization problem is convex. The initial values satisfy the constraints. However, for different given parameters, sometimes CVX failed to find the optimal solution, sometimes it works.
Please see the following Matlab code and CVX status below.
Thanks for the possible reply and help.

Please note that there are only four variables, i.e., variables Pu P1 P2 P3. The other parameters are all positive.

A =[1 0 0 0 ;
HDU’ c_P];
b = [power_UAVMAX c_b ];
cvx_begin %quiet
variables Pu P1 P2 P3
minimize( Enemy_Loss_FactorR0FIX1exp(-log(1+HDU_enemyPu/gain_enemy)) - B./log(2)*…
(log(p_N0 + Pu.*HDU_user1 + HD_user1_user1ToM(1).*P1 + HD_user1_user1ToM(2).*P2 +HD_user1_user1ToM(3).*P3) +…
log(p_N0 + Pu.*HDU_user2 + HD_user2_user1ToM(1).*P1 + HD_user2_user1ToM(2).*P2 +HD_user2_user1ToM(3).*P3) +…
log(p_N0 + Pu.*HDU_user3 + HD_user3_user1ToM(1).*P1 + HD_user3_user1ToM(2).*P2 +HD_user3_user1ToM(3).P3)) + B./log(2)…
(log(p_N0 + Pu0.*HDU_user1 + HD_user1_user1ToM(2).*P0(2) + HD_user1_user1ToM(3).*P0(3))+…
log(p_N0 + Pu0.*HDU_user2 + HD_user2_user1ToM(1).*P0(1) + HD_user2_user1ToM(3).*P0(3))+…
log(p_N0 + Pu0.HDU_user3 + HD_user3_user1ToM(1).P0(1) + HD_user3_user1ToM(2).P0(2) )) + B./log(2).…
((HDU_user1.(Pu-Pu0) + HD_user1_user1ToM.( [P1,P2,P3] - P0 )Index1)./(p_N0 + Pu0.HDU_user1 + HD_user1_user1ToM.P0Index1)+… % i = 1
(HDU_user2.(Pu-Pu0) + HD_user2_user1ToM.( [P1,P2,P3] - P0 )Index2)./(p_N0 + Pu0.HDU_user2 + HD_user2_user1ToM.P0Index2)+… % i = 2
(HDU_user3.(Pu-Pu0) + HD_user3_user1ToM.( [P1,P2,P3] - P0 )*Index3)./(p_N0 + Pu0.*HDU_user3 + HD_user3_user1ToM.P0Index3)) % i = 3

subject to
A(1,:)*[Pu P1 P2 P3]'<= b(1)
A(2,:)*[Pu P1 P2 P3]'<= b(2)
A(3,:)*[Pu P1 P2 P3]'<= b(3)
A(4,:)*[Pu P1 P2 P3]'<= b(4)

Pu<=Pu_max
P1<=P1_max;
P2<=P2_max;
P3<=P3_max;
0<=Pu
0<=P2
0<=P3
0<=P1

cvx_end

Successive approximation method to be employed.
For improved efficiency, SDPT3 is solving the dual problem.
SDPT3 will be called several times to refine the solution.
Original size: 24 variables, 8 equality constraints
4 exponentials add 32 variables, 20 equality constraints

Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed

Status: Failed
Optimal value (cvx_optval): NaN

Christ · July 3, 2019, 1:09pm

Please note that the constraints in the left side of all inequations are linear w.r.t. all variables.

Mark_L_Stone · July 3, 2019, 1:26pm

Please follow the advice in CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions and tell us what happens.

Christ · July 3, 2019, 2:26pm

Dear Sir:

Thanks so much for the reply. I have folllowed your suggestion. But the problem is still unsloved. Please find the revisions on the Matlab codes and the CVX status below:

A =[1 0 0 0 ;
    HDU'  c_P];
b = [power_UAVMAX c_b ];
cvx_begin %quiet
    variables Pu P1 P2 P3   z
     minimize(  Enemy_Loss_Factor*R0*(FIX1*exp(z)-  1)- B./log(2)*...%  
    (-rel_entr(1,p_N0 + Pu.*HDU_user1 + HD_user1_user1ToM(1).*P1 + HD_user1_user1ToM(2).*P2 +HD_user1_user1ToM(3).*P3) +...
     -rel_entr(1,p_N0 + Pu.*HDU_user2 + HD_user2_user1ToM(1).*P1 + HD_user2_user1ToM(2).*P2 +HD_user2_user1ToM(3).*P3) +...
     -rel_entr(1,p_N0 + Pu.*HDU_user3 + HD_user3_user1ToM(1).*P1 + HD_user3_user1ToM(2).*P2 +HD_user3_user1ToM(3).*P3))    +    B./log(2)*...%%  
       (-rel_entr(1,p_N0 + Pu0.*HDU_user1 + HD_user1_user1ToM(2).*P0(2) + HD_user1_user1ToM(3).*P0(3))+...
     -rel_entr(1,p_N0 + Pu0.*HDU_user2 + HD_user2_user1ToM(1).*P0(1) + HD_user2_user1ToM(3).*P0(3))+...
     -rel_entr(1,p_N0 + Pu0.*HDU_user3 + HD_user3_user1ToM(1).*P0(1) + HD_user3_user1ToM(2).*P0(2) ))   +   B./log(2).*...  %% 
    (HDU_user2.*(Pu-Pu0) + HD_user2_user1ToM.*( [P1,P2,P3] - P0 )*Index2)./(p_N0 + Pu0.*HDU_user2 + HD_user2_user1ToM.*P0*Index2)+... % 
    (HDU_user3.*(Pu-Pu0) + HD_user3_user1ToM.*( [P1,P2,P3] - P0 )*Index3)./(p_N0 + Pu0.*HDU_user3 + HD_user3_user1ToM.*P0*Index3))
 
 
    subject to
    A(1,:)*[Pu P1 P2 P3]'<= b(1)
    A(2,:)*[Pu P1 P2 P3]'<= b(2)
    A(3,:)*[Pu P1 P2 P3]'<= b(3)
    A(4,:)*[Pu P1 P2 P3]'<= b(4)

    Pu<=Pu_max
    P1<=P1_max;
    P2<=P2_max;
    P3<=P3_max;
    0<=Pu
    0<=P2
    0<=P3
    0<=P1
    
    rel_entr(1,1+HDU_enemy*Pu/gain_enemy) + rel_entr(1,z) <= 0
    
cvx_end

===========================================

Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

Calling SDPT3 4.0: 108 variables, 40 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.

num. of constraints = 40
dim. of sdp var = 60, num. of sdp blk = 30
dim. of linear var = 18

SDPT3: Infeasible path-following algorithms

version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

0|0.000|0.000|1.1e+02|4.5e+00|9.9e+03| 5.089943e+02 0.000000e+00| 0:0:00| chol 1 1
1|0.851|0.563|1.7e+01|2.0e+00|4.3e+03| 1.409194e+02 -1.006672e-01| 0:0:00| chol 1 1
2|0.774|0.058|3.9e+00|1.9e+00|5.7e+03|-7.861046e+04 -1.279831e-01| 0:0:00| chol 1 1
3|0.003|0.003|3.8e+00|1.9e+00|2.5e+04|-5.717612e+06 -1.363012e-01| 0:0:00| chol 1 1
4|0.000|0.000|3.8e+00|1.9e+00|2.8e+05|-8.064303e+07 -1.379926e-01| 0:0:00| chol 1 1
5|0.000|0.000|3.8e+00|1.9e+00|4.5e+06|-1.330844e+09 -1.455830e-01| 0:0:00| chol 1 1
6|0.000|0.000|3.8e+00|1.9e+00|7.7e+07|-2.338328e+10 -3.705110e-01| 0:0:00| chol 1 1
7|0.001|0.000|3.8e+00|1.9e+00|5.5e+09|-1.713226e+12 -6.582823e-01| 0:0:00| chol 1 1
8|0.000|0.000|3.8e+00|1.9e+00|5.9e+09|-1.828916e+12 -1.078281e+01| 0:0:00| chol 1 1
9|0.000|0.000|3.8e+00|1.9e+00|2.4e+10|-7.341693e+12 -3.391826e+01| 0:0:00| chol 1 1
10|0.000|0.000|3.8e+00|1.9e+00|3.1e+10|-9.838339e+12 -2.357456e+02| 0:0:00| chol 1 1
11|0.000|0.000|3.8e+00|1.9e+00|1.1e+11|-3.514938e+13 -6.455584e+02| 0:0:00| chol 1 1
12|0.000|0.000|3.8e+00|1.8e+00|1.7e+12|-5.454215e+14 -2.031936e+03| 0:0:00| chol 2 2
13|0.000|0.000|3.8e+00|1.8e+00|2.6e+12|-8.344291e+14 -1.174112e+04| 0:0:00| chol 1 2
14|0.000|0.000|3.8e+00|1.8e+00|2.3e+13|-7.344683e+15 -2.910909e+04| 0:0:00| chol 2 2
15|0.000|0.000|3.8e+00|1.8e+00|2.9e+13|-9.178724e+15 -2.108064e+05| 0:0:00| chol 1 2
16|0.000|0.000|3.8e+00|1.8e+00|1.8e+14|-5.765527e+16 -1.032091e+06| 0:0:00| chol 2 2
17|0.000|0.000|3.8e+00|1.8e+00|3.6e+15|-1.192047e+18 -2.575840e+06| 0:0:00| chol 2 2
18|0.000|0.000|3.8e+00|1.8e+00|4.7e+15|-1.568195e+18 -1.274923e+07| 0:0:00|
sqlp stop: primal or dual is diverging, 1.2e+15

number of iterations = 18
Total CPU time (secs) = 0.33
CPU time per iteration = 0.02
termination code = 3
DIMACS: 3.8e+00 0.0e+00 3.0e+00 0.0e+00 -1.0e+00 3.0e-03

Status: Failed
Optimal value (cvx_optval): NaN

Mark_L_Stone · July 3, 2019, 2:34pm

You haven’t provided the input data. Therefore your problem is not reproducible.

Based on the output, we can see that, as intended, CVXQUAD’s Pade Approxiimant was invoked instead of CVX’s Successive Approximation method.

Apparently, your problem is too numerically difficult for SDPT3 to successfully handle. A common culprit is badly scaled o ill-conditioned input data. Any non-zero input numbers having very large or small magnitude are likely candidates for causing or contributing to the difficulties.

It is possible that Mosek might perform better as solver than SDPT3, and might provide better diagnostic information and warnings.

Christ · July 3, 2019, 2:53pm

Thanks a lot for your time, Sir. The problem has confused us for quite a period.
We also tried Mosek several days ago, which neither worked.
The overall programmes include seven .m files.
Shall we post them here? or just send it to your mailbox?

Mark_L_Stone · July 3, 2019, 3:07pm

If you run Mosek under the CVXQUAD formulation and show all the output, perhaps readers will get some insights on problem difficulties, such as scaling.

Have you examined the magnitudes of all input data?

On this forum, we keep communications to what can be conveyed on the forum., without use of email or posting of data on external sites.

Christ · July 3, 2019, 3:24pm

Another problem seems weird.
In what follows, we can see that CVXQUAD’s Pade Approxiimant was invoked instead of CVX’s Successive Approximation method.

CVX Warning:
Models involving “rel_entr” or other functions in the log, exp, and entropy
family are solved using an experimental successive approximation method.
This method is slower and less reliable than the method CVX employs for
other models. Please see the section of the user’s guide entitled
The successive approximation method
for more details about the approach, and for instructions on how to
suppress this warning message in the future.

Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

However, after that, we have the following status, which indicates that SDPT3 is also invoked. Is that right?

Calling SDPT3 4.0: 108 variables, 40 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.

num. of constraints = 40
dim. of sdp var = 60, num. of sdp blk = 30
dim. of linear var = 18

SDPT3: Infeasible path-following algorithms

version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

Christ · July 3, 2019, 3:34pm

Following your suggestion, we have just found that the scaling indeed matters. If we change the coefficients in the objective function, the optimization problem maybe be solved with CVXQUAD. But then, the coefficient does not make sense in the practical problem. Maybe we need some tricks to deal with it appropriately.

Mark_L_Stone · July 3, 2019, 3:35pm

This shws that CVQUAD’s Pade Approximant was invoked and CVX’s Successive Approcimation method was not used. For this problem, CVXQUAD formulates LMIs (SDP constraints) which get added to the problem formulation. CVX transforms those to Second Order Cone constraints, and then calls a solver, in this case SDPT3. The CVX Warning message is because CVXQUAD and CVX were developed by different developers and are not tightly integrated - despite this warning, CVX’s Successive Approximation method was not actually used. If CVXQUAD and CVX were better integrated, the user wouldn’t need to use the reformulation tricks in the link I provided.

Regarding scaling, you should try to make offsetting changes to preserve the “correctness”: of your model. For instance, change the units of mm to km.

Christ · July 3, 2019, 3:37pm

get it. Thanks for the explaination.

Christ · July 8, 2019, 9:29am

Dear Mark:

We are turning to you for more help. We are trying to solve another optimization problem as below

Please note that the highlighted symbols are variables. We have followed your advice: follow the advice in CVXQUAD: How to use CVXQUAD’s Pade Approximant instead of CVX’s unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone.

The following is the matlab code and resulting status:

A =[1 0 0 0 ;
HPU’ c_P];
b = [power_UAVMAX c_b ];

cvx_begin %quiet

variables S_ue  S_u1 S_u2 S_u3 S_uu0 Xu Yu Z1 Z2 Z3 Z4 

    minimize(  Enemy_Loss_Factor*R0*(FIX1*Z1  -  1)- B/log(2)*...
        (-rel_entr(1,p_N0 + S_u1.*HPU_user1 + HD_user1_user1ToM*P0'))+B/(log(2))*...
        (-rel_entr(1,p_N0 + S_u1_0.*HPU_user1 + HD_user1_user1ToM.*P0*Index1))+B./log(2).*...  
       (((S_u1-S_u1_0).*HPU_user1 )./(p_N0 + S_u1_0.*HPU_user1 +                         
        HD_user1_user1ToM.*P0*Index1)+...% i = 1
        (S_uu0./Dist0).^K+(S_uu0 ./ V0))

    subject to

      (Xu - X_loc_enemy).^2 + (Yu - Y_loc_enemy).^2 <= 1./S_ue_0 - 1./S_ue_0.^2.*(Z1 - 1./S_ue_0)

     rel_entr(1,S_ue) + rel_entr(1,Z1) <= 0

      Z2<= (Xu_0 - X_loc_user1).^2 + (Yu_0 - Y_loc_user1).^2 + 2*(Xu_0 - X_loc_user1).*(Xu - Xu_0) +2*(Yu_0 - Y_loc_user1).*(Yu - Yu_0)

    rel_entr(1,  S_u1  ) + rel_entr(1,Z2) <= 0

     Z3<= (Xu_0 - X_loc_user1).^2 + (Yu_0 - Y_loc_user1).^2 + 2*(Xu_0 - X_loc_user1).*(Xu - Xu_0) +2*(Yu_0 - Y_loc_user1).*(Yu - Yu_0)

     rel_entr(1,  S_u2  ) + rel_entr(1,Z3) <= 0

    Z4<= (Xu_0 - X_loc_user1).^2 + (Yu_0 - Y_loc_user1).^2 + (Xu_0 - X_loc_user1).*(Xu - Xu_0) +(Yu_0 - Y_loc_user1).*(Yu - Yu_0)

     rel_entr(1,  S_u3  ) + rel_entr(1,Z4) <= 0

     (Xu - X_logc_U0).^2 + (Yu - Y_logc_U0).^2 <= S_uu0_0.^2 + 2*S_uu0_0*(S_uu0 -S_uu0_0)
      
     S_u1.*HPU(1) + c_P(1,:)*(P0') <= c_b(1)
     S_u2.*HPU(2) + c_P(2,:)*(P0') <= c_b(2)
     S_u3.*HPU(3) + c_P(3,:)*(P0') <= c_b(3)
     

     rel_entr(1,1+HPU_enemy.*S_ue./gain_enemy) + rel_entr(1,Z1) <= 0
     
    cvx_end

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================

Calling SDPT3 4.0: 279 variables, 107 equality constraints
** For improved efficiency, SDPT3 is solving the dual problem.**
------------------------------------------------------------

** num. of constraints = 107**
** dim. of sdp var = 166, num. of sdp blk = 83**
** dim. of linear var = 30**
** number of nearly dependent constraints = 106**
** To remove these constraints, re-run sqlp.m with OPTIONS.rmdepconstr = 1.**

** SDPT3: Infeasible path-following algorithms**

** version predcorr gam expon scale_data**
** HKM 1 0.000 1 0 **
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
-------------------------------------------------------------------
** 0|0.000|0.000|2.2e+14|1.0e+00|2.6e+33| 1.281612e+33 0.000000e+00| 0:0:00| chol 2 * 3 **
** 1|0.000|0.000|2.2e+14|1.0e+00|2.6e+33| 1.281612e+33 -2.340504e+13| 0:0:00| chol 2 * 3 **
** 2|0.000|0.000|2.2e+14|1.0e+00|2.6e+33| 1.281612e+33 -1.808893e+14| 0:0:00| chol 2 * 3 **
** 3|0.000|0.000|2.2e+14|1.0e+00|2.6e+33| 1.281612e+33 -3.946221e+14| 0:0:00| chol 2 * 3 **
** 4|0.000|0.000|2.2e+14|1.0e+00|2.6e+33| 1.281612e+33 -1.993101e+15| 0:0:00|**
** *** Too many tiny steps: restarting with the following iterate.**
** *** [X,y,Z] = infeaspt(blk,At,C,b,2,1e5); chol * 3 * 3 **
** 5|0.000|0.000|4.0e+07|1.0e+00|3.0e+12| 2.326203e+26 -2.085650e+18| 0:0:00|**
** *** Too many tiny steps even after restarting**
** stop: steps too short consecutively***
-------------------------------------------------------------------
** number of iterations = 5**
** primal objective value = 2.32620313e+26**
** dual objective value = 0.00000000e+00**
** gap := trace(XZ) = 1.96e+12**
** relative gap = 8.43e-15**
** actual relative gap = 1.00e+00**
** rel. primal infeas (scaled problem) = 4.00e+07**
** rel. dual " " " = 1.00e+00**
** rel. primal infeas (unscaled problem) = 0.00e+00**
** rel. dual " " " = 0.00e+00**
** norm(X), norm(y), norm(Z) = 1.4e+06, 0.0e+00, 1.4e+06**
** norm(A), norm(b), norm© = 1.8e+14, 4.4e+11, 2.3e+21**
** Total CPU time (secs) = 0.30 **
** CPU time per iteration = 0.06 **
** termination code = -5**
** DIMACS: 6.4e+07 0.0e+00 1.0e+00 0.0e+00 1.0e+00 8.4e-15**
-------------------------------------------------------------------

------------------------------------------------------------
Status: Failed
Optimal value (cvx_optval): NaN

Thanks a lot for your time!

Mark_L_Stone · July 8, 2019, 9:45am

This is not a reproducible code, so I have no idea what has happened, other than that SDPT3 had numerical difficulties and the clue that SDPT3 reports

number of nearly dependent constraints = 106
** To remove these constraints, re-run sqlp.m with OPTIONS.rmdepconstr = 1.

You can implement this suggestion by including
cvx_solver_settings('rmdepconstr',1)
in your code.

You should also check the input data for non-zero elements which are much smaller or larger than one in magnitude. As before, bad scaling is a possible contributor to the solver’s difficulties.

You could also try SeDuMi. Gurobi or Mosek might have a better chance of success, or at least, provide more diagnostic information.

Christ · July 8, 2019, 10:06am

Thanks for the suggestion. I have just added

cvx_solver_settings(‘rmdepconstr’,1)

into the Matlab code, as can be seen from below figure:

However, it does not work(the resulting status is given below).

> =====================================
> =====================================
> Using Pade approximation for exponential
> cone with parameters m=3, k=3
> =====================================
> =====================================
> Using Pade approximation for exponential
> cone with parameters m=3, k=3
> =====================================
> =====================================
> Using Pade approximation for exponential
> cone with parameters m=3, k=3
> =====================================
> =====================================
> Using Pade approximation for exponential
> cone with parameters m=3, k=3
> =====================================
> =====================================
> Using Pade approximation for exponential
> cone with parameters m=3, k=3
> =====================================
> =====================================
> Using Pade approximation for exponential
> cone with parameters m=3, k=3
> =====================================
> =====================================
> Using Pade approximation for exponential
> cone with parameters m=3, k=3
> =====================================
> =====================================
> Using Pade approximation for exponential
> cone with parameters m=3, k=3
> =====================================
> =====================================
> Using Pade approximation for exponential
> cone with parameters m=3, k=3
> =====================================
**> **
> Calling SDPT3 4.0: 279 variables, 107 equality constraints
> For improved efficiency, SDPT3 is solving the dual problem.
> ------------------------------------------------------------
> NOTE: custom settings have been set for this solver.
> ------------------------------------------------------------
**> **
> num. of constraints = 107
> dim. of sdp var = 166, num. of sdp blk = 83
> dim. of linear var = 30
> number of nearly dependent constraints = 106
> checkdepconstr: removing dependent constraints…
> checkdepconstr: basis rows cannot be reliably identified, abort removing nearly dependent constraints
**> *********************************************************************
> SDPT3: Infeasible path-following algorithms
**> *********************************************************************
> version predcorr gam expon scale_data
**> HKM 1 0.000 1 0 **
> it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
> -------------------------------------------------------------------
**> 0|0.000|0.000|2.2e+14|1.0e+00|2.6e+33| 1.281612e+33 0.000000e+00| 0:0:00| chol 2 * 3 **
**> 1|0.000|0.000|2.2e+14|1.0e+00|2.6e+33| 1.281612e+33 -2.340504e+13| 0:0:00| chol 2 * 3 **
**> 2|0.000|0.000|2.2e+14|1.0e+00|2.6e+33| 1.281612e+33 -1.808893e+14| 0:0:00| chol 2 * 3 **
**> 3|0.000|0.000|2.2e+14|1.0e+00|2.6e+33| 1.281612e+33 -3.946221e+14| 0:0:00| chol 2 * 3 **
> 4|0.000|0.000|2.2e+14|1.0e+00|2.6e+33| 1.281612e+33 -1.993101e+15| 0:0:00|
> *** Too many tiny steps: restarting with the following iterate.
*> *** [X,y,Z] = infeaspt(blk,At,C,b,2,1e5); chol * 3 * 3 **
> 5|0.000|0.000|4.0e+07|1.0e+00|3.0e+12| 2.326203e+26 -2.085650e+18| 0:0:00|
> *** Too many tiny steps even after restarting
> stop: steps too short consecutively
> -------------------------------------------------------------------
> number of iterations = 5
> primal objective value = 2.32620313e+26
> dual objective value = 0.00000000e+00
> gap := trace(XZ) = 1.96e+12
> relative gap = 8.43e-15
> actual relative gap = 1.00e+00
> rel. primal infeas (scaled problem) = 4.00e+07
> rel. dual " " " = 1.00e+00
> rel. primal infeas (unscaled problem) = 0.00e+00
> rel. dual " " " = 0.00e+00
> norm(X), norm(y), norm(Z) = 1.4e+06, 0.0e+00, 1.4e+06
> norm(A), norm(b), norm© = 1.8e+14, 4.4e+11, 2.3e+21
**> Total CPU time (secs) = 0.31 **
**> CPU time per iteration = 0.06 **
> termination code = -5
> DIMACS: 6.4e+07 0.0e+00 1.0e+00 0.0e+00 1.0e+00 8.4e-15
> -------------------------------------------------------------------
**> **
> ------------------------------------------------------------
> Status: Failed
> Optimal value (cvx_optval): NaN

**Then I delete the first two constraints which are corresponding to inequation (44), i.e., **

(Xu - X_loc_enemy).^2 + (Yu - Y_loc_enemy).^2 <= 1./S_ue_0 - 1./S_ue_0.^2.*(Z1 - 1./S_ue_0)

rel_entr(1,S_ue) + rel_entr(1,Z1) <= 0

The problem can not be solved in the first round, however, in the second and sequetial rounds, it can be solved succesfully, as can be seen below:

** =====================================**
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================

Calling SDPT3 4.0: 233 variables, 91 equality constraints
** For improved efficiency, SDPT3 is solving the dual problem.**
------------------------------------------------------------
NOTE: custom settings have been set for this solver.
------------------------------------------------------------

** num. of constraints = 91**
** dim. of sdp var = 138, num. of sdp blk = 69**
** dim. of linear var = 26**

** SDPT3: Infeasible path-following algorithms**

** version predcorr gam expon scale_data**
** HKM 1 0.000 1 0 **
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
-------------------------------------------------------------------
** 0|0.000|0.000|3.5e+04|2.2e+00|4.1e+19|-2.023465e+19 0.000000e+00| 0:0:00| chol 2 2 **
** 1|0.000|0.000|3.5e+04|2.2e+00|4.1e+19|-2.023313e+19 -2.332384e+13| 0:0:00| chol 2 2 **
** 2|0.000|0.000|3.5e+04|2.2e+00|4.1e+19|-2.023092e+19 -2.171174e+14| 0:0:00| chol 2 2 **
** 3|0.000|0.000|3.5e+04|2.2e+00|4.1e+19|-2.022030e+19 -4.194465e+14| 0:0:00| chol 2 2 **
** 4|0.001|0.003|3.5e+04|2.2e+00|4.1e+19|-2.020112e+19 -3.228699e+15| 0:0:00|**
** *** Too many tiny steps: restarting with the following iterate.**
** *** [X,y,Z] = infeaspt(blk,At,C,b,2,1e5); chol 1 2 **
** 5|0.000|0.000|1.0e+00|1.0e+00|2.6e+12|-3.674090e+12 -2.085650e+18| 0:0:00|**
** *** Too many tiny steps even after restarting**
** stop: steps too short consecutively***
-------------------------------------------------------------------
** number of iterations = 5**
** primal objective value = -3.67408969e+12**
** dual objective value = -2.08565042e+18**
** gap := trace(XZ) = 2.65e+12**
** relative gap = 1.27e-06**
** actual relative gap = 1.00e+00**
** rel. primal infeas (scaled problem) = 1.00e+00**
** rel. dual " " " = 1.01e+00**
** rel. primal infeas (unscaled problem) = 0.00e+00**
** rel. dual " " " = 0.00e+00**
** norm(X), norm(y), norm(Z) = 1.3e+06, 4.8e+06, 5.3e+06**
** norm(A), norm(b), norm© = 1.6e+04, 4.4e+11, 2.1e+07**
** Total CPU time (secs) = 0.30 **
** CPU time per iteration = 0.06 **
** termination code = -5**
** DIMACS: 1.6e+00 0.0e+00 1.7e+00 0.0e+00 1.0e+00 1.3e-06**
-------------------------------------------------------------------

------------------------------------------------------------
Status: Failed
Optimal value (cvx_optval): NaN

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================

Calling SDPT3 4.0: 233 variables, 91 equality constraints
** For improved efficiency, SDPT3 is solving the dual problem.**
------------------------------------------------------------
NOTE: custom settings have been set for this solver.
------------------------------------------------------------

** num. of constraints = 91**
** dim. of sdp var = 138, num. of sdp blk = 69**
** dim. of linear var = 26**

** SDPT3: Infeasible path-following algorithms**

** version predcorr gam expon scale_data**
** HKM 1 0.000 1 0 **
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
-------------------------------------------------------------------
** 0|0.000|0.000|7.5e+03|1.0e+00|3.6e+18| 1.688756e+18 0.000000e+00| 0:0:00| chol 2 2 **
** 1|0.001|0.001|7.5e+03|1.0e+00|3.6e+18| 1.686681e+18 -2.369304e+13| 0:0:00| chol 2 2 **
** 2|0.002|0.005|7.5e+03|9.9e-01|3.6e+18| 1.683740e+18 -2.196155e+14| 0:0:00| chol 2 2 **
** 3|0.010|0.006|7.4e+03|9.9e-01|3.6e+18| 1.668505e+18 -4.267657e+14| 0:0:00| chol 2 2 **
** 4|0.019|0.062|7.3e+03|9.3e-01|3.5e+18| 1.638604e+18 -3.007115e+15| 0:0:00| chol 2 2 **
** 5|0.187|0.054|5.9e+03|8.8e-01|3.3e+18| 1.348677e+18 -4.276196e+15| 0:0:00| chol 2 2 **
** 6|0.166|0.338|5.0e+03|5.8e-01|2.7e+18| 1.139477e+18 -1.847051e+16| 0:0:00| chol 2 2 **
** 7|0.754|0.719|1.2e+03|1.6e-01|8.5e+17| 3.291484e+17 -1.593915e+16| 0:0:00| chol 2 2 **
** 8|0.792|0.651|2.5e+02|5.7e-02|3.4e+17| 1.224091e+17 -1.052687e+16| 0:0:00| chol 2 2 **
** 9|0.811|0.857|4.8e+01|8.2e-03|6.9e+16| 3.716348e+16 -1.714011e+15| 0:0:00| chol 2 2 **
**10|0.788|0.473|1.0e+01|4.3e-03|3.9e+16| 1.930476e+16 -1.131258e+15| 0:0:00| chol 2 2 **
**11|0.632|0.823|3.8e+00|7.6e-04|1.7e+16| 1.189954e+16 -1.892313e+14| 0:0:00| chol 2 2 **
**12|0.815|0.609|7.0e-01|3.0e-04|6.1e+15| 4.242271e+15 -1.091545e+14| 0:0:00| chol 2 2 **
**13|0.736|0.819|1.8e-01|5.4e-05|2.4e+15| 1.936973e+15 -4.299005e+13| 0:0:00| chol 2 2 **
**14|0.606|0.543|7.3e-02|2.5e-05|1.4e+15| 1.069730e+15 -3.757119e+13| 0:0:00| chol 2 2 **
**15|0.669|0.779|2.4e-02|5.5e-06|8.1e+14| 6.085669e+14 -2.762333e+13| 0:0:00| chol 2 2 **
**16|0.587|0.621|9.9e-03|2.1e-06|5.1e+14| 3.558779e+14 -2.145224e+13| 0:0:00| chol 2 2 **
**17|0.558|0.751|4.4e-03|5.5e-07|3.3e+14| 2.375757e+14 -1.617851e+13| 0:0:00| chol 2 2 **
**18|0.904|0.879|4.2e-04|7.6e-08|6.4e+13| 4.553967e+13 -4.817909e+12| 0:0:00| chol 2 2 **
**19|0.558|0.796|1.8e-04|2.4e-08|4.2e+13| 3.070416e+13 -2.890987e+12| 0:0:00| chol 2 2 **
**20|0.921|0.877|1.5e-05|5.1e-09|9.5e+12| 6.764841e+12 -9.069696e+11| 0:0:00| chol 2 2 **
**21|0.852|0.828|2.2e-06|1.7e-09|4.0e+12| 2.863848e+12 -4.058692e+11| 0:0:00| chol 2 2 **
**22|0.760|0.892|5.2e-07|4.6e-10|1.4e+12| 1.049945e+12 -1.180939e+11| 0:0:00| chol 2 2 **
**23|0.692|0.731|1.6e-07|2.4e-10|7.8e+11| 5.453558e+11 -8.044132e+10| 0:0:00| chol 2 2 **
**24|0.811|0.891|3.0e-08|6.0e-11|2.5e+11| 1.662367e+11 -3.847266e+10| 0:0:00| chol 2 2 **
**25|0.795|0.792|6.2e-09|2.6e-11|1.1e+11| 6.086836e+10 -2.997054e+10| 0:0:00| chol 2 2 **
**26|0.783|0.890|1.4e-09|7.5e-12|3.9e+10| 9.819369e+09 -2.353004e+10| 0:0:00| chol 2 2 **
**27|0.724|0.780|3.7e-10|4.4e-12|2.2e+10|-3.892263e+09 -2.248423e+10| 0:0:00| chol 2 2 **
28|0.827|0.970|6.5e-11|1.2e-12|6.6e+09|-1.534949e+10 -2.119441e+10| 0:0:00| chol 2 2 **
29|0.885|1.000|7.4e-12|5.0e-13|1.6e+09|-1.947948e+10 -2.092088e+10| 0:0:00| chol 2 2 **
30|0.804|1.000|1.5e-12|3.6e-13|5.0e+08|-2.038982e+10 -2.084066e+10| 0:0:00| chol 2 2 **
31|0.824|1.000|2.6e-13|3.2e-13|1.6e+08|-2.067427e+10 -2.081698e+10| 0:0:00| chol 2 2 **
32|0.788|1.000|5.4e-14|2.9e-13|5.3e+07|-2.075788e+10 -2.080617e+10| 0:0:00| chol 2 2 **
33|0.811|1.000|1.0e-14|3.1e-13|2.0e+07|-2.078570e+10 -2.080349e+10| 0:0:00| chol 2 1 **
34|0.824|1.000|1.8e-15|2.5e-13|5.7e+06|-2.079657e+10 -2.080169e+10| 0:0:00| chol 1 1 **
35|0.780|1.000|8.3e-16|2.5e-13|2.5e+06|-2.079912e+10 -2.080141e+10| 0:0:00| chol 2 2 **
36|0.828|0.999|6.2e-16|1.4e-13|7.2e+05|-2.080046e+10 -2.080111e+10| 0:0:00| chol 2 2 **
37|0.712|1.000|5.1e-16|1.2e-13|4.6e+05|-2.080067e+10 -2.080108e+10| 0:0:00| chol 2 2 **
38|0.749|1.000|3.7e-16|6.2e-14|2.1e+05|-2.080083e+10 -2.080102e+10| 0:0:00| chol 2 1 **
39|0.822|1.000|1.9e-16|2.9e-14|9.5e+04|-2.080091e+10 -2.080100e+10| 0:0:00| chol 2 2 **
40|0.874|0.973|4.6e-16|6.7e-15|1.9e+04|-2.080096e+10 -2.080098e+10| 0:0:00|# chol 2 2 **
41|0.951|0.988|7.0e-16|1.9e-15|3.7e+03|-2.080097e+10 -2.080097e+10| 0:0:00|# chol 2 2 **
42|1.000|1.000|4.6e-16|3.8e-16|1.2e+03|-2.080097e+10 -2.080097e+10| 0:0:00|# chol 2 2 **
43|0.921|0.987|1.1e-15|8.6e-16|2.3e+02|-2.080097e+10 -2.080097e+10| 0:0:00|
** stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
** number of iterations = 43
** primal objective value = -2.08009702e+10
** dual objective value = -2.08009704e+10
** gap := trace(XZ) = 2.30e+02
** relative gap = 5.54e-09
** actual relative gap = 4.90e-09
** rel. primal infeas (scaled problem) = 1.09e-15
** rel. dual " " " = 8.61e-16
** rel. primal infeas (unscaled problem) = 0.00e+00
** rel. dual " " " = 0.00e+00
** norm(X), norm(y), norm(Z) = 1.1e+12, 8.3e+12, 8.3e+12
** norm(A), norm(b), norm© = 3.5e+03, 4.4e+11, 1.7e+06
** Total CPU time (secs) = 0.24 **
** CPU time per iteration = 0.01 **
** termination code = 0
** DIMACS: 1.7e-15 0.0e+00 1.5e-15 0.0e+00 4.9e-09 5.5e-09
-------------------------------------------------------------------

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): -1.23798e+18

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================

Calling SDPT3 4.0: 233 variables, 91 equality constraints
** For improved efficiency, SDPT3 is solving the dual problem.**
------------------------------------------------------------
NOTE: custom settings have been set for this solver.
------------------------------------------------------------

** num. of constraints = 91**
** dim. of sdp var = 138, num. of sdp blk = 69**
** dim. of linear var = 26**

** SDPT3: Infeasible path-following algorithms**

** version predcorr gam expon scale_data**
** HKM 1 0.000 1 0 **
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
-------------------------------------------------------------------
** 0|0.000|0.000|2.3e+04|2.2e+00|1.7e+15|-8.292009e+14 0.000000e+00| 0:0:00| chol 1 2 **
** 1|0.000|0.000|2.3e+04|2.2e+00|1.7e+15|-8.291349e+14 -3.290357e+09| 0:0:00| chol 1 2 **
** 2|0.000|0.000|2.3e+04|2.2e+00|1.7e+15|-8.290394e+14 -1.882718e+10| 0:0:00| chol 1 2 **
** 3|0.001|0.000|2.3e+04|2.2e+00|1.7e+15|-8.285748e+14 -3.565843e+10| 0:0:00| chol 2 2 **
** 4|0.001|0.003|2.3e+04|2.2e+00|1.7e+15|-8.277512e+14 -2.193466e+11| 0:0:00|**
** *** Too many tiny steps: restarting with the following iterate.**
** *** [X,y,Z] = infeaspt(blk,At,C,b,2,1e5); chol 1 1 **
** 5|0.621|0.578|3.8e+01|4.3e-01|2.6e+17|-1.359567e+12 -4.156501e+17| 0:0:00| chol 1 2 **
** 6|0.000|0.000|3.8e+01|4.3e-01|2.6e+17|-1.356623e+12 -4.156194e+17| 0:0:00| chol 1 2 **
** 7|0.000|0.000|3.8e+01|4.3e-01|2.6e+17|-1.349707e+12 -4.155994e+17| 0:0:00| chol 1 2 **
** 8|0.001|0.000|3.8e+01|4.3e-01|2.6e+17|-1.270517e+12 -4.155541e+17| 0:0:00| chol 1 2 **
** 9|0.002|0.004|3.8e+01|4.2e-01|2.6e+17|-1.189136e+12 -4.146214e+17| 0:0:00| chol 1 2 **
**10|0.009|0.002|3.7e+01|4.2e-01|2.6e+17| 2.868385e+11 -4.141717e+17| 0:0:00| chol 1 1 **
**11|0.012|0.020|3.7e+01|4.2e-01|2.6e+17| 1.388974e+12 -4.089875e+17| 0:0:00| chol 1 2 **
**12|0.010|0.009|3.7e+01|4.1e-01|2.6e+17| 1.916318e+13 -4.068034e+17| 0:0:00| chol 1 1 **
**13|0.285|0.090|2.6e+01|3.7e-01|2.9e+17| 9.328410e+13 -3.825058e+17| 0:0:00| chol 1 2 **
**14|0.478|0.674|1.4e+01|1.2e-01|1.4e+17| 1.604177e+14 -1.580122e+17| 0:0:00| chol 1 1 **
**15|0.688|0.226|4.3e+00|9.4e-02|1.5e+17| 7.920949e+14 -1.241986e+17| 0:0:00| chol 2 2 **
**16|0.660|0.451|1.5e+00|5.2e-02|9.3e+16| 9.909623e+14 -6.972369e+16| 0:0:00| chol 2 2 **
**17|0.785|0.905|3.1e-01|4.9e-03|9.6e+15| 4.785442e+14 -6.827212e+15| 0:0:00| chol 2 2 **
**18|0.532|0.431|1.5e-01|2.8e-03|7.1e+15| 3.319514e+14 -4.090253e+15| 0:0:00| chol 2 2 **
**19|0.920|0.906|1.2e-02|2.6e-04|7.4e+14| 5.851464e+13 -4.111651e+14| 0:0:00| chol 2 2 **
**20|0.910|0.610|1.0e-03|1.0e-04|4.1e+14| 3.671482e+13 -1.757251e+14| 0:0:00| chol 2 2 **
**21|0.540|0.802|4.8e-04|2.0e-05|1.3e+14| 2.882051e+13 -4.126427e+13| 0:0:00| chol 2 2 **
**22|0.814|0.790|9.0e-05|4.3e-06|4.6e+13| 1.782912e+13 -1.129282e+13| 0:0:00| chol 2 2 **
**23|0.889|0.903|9.9e-06|4.3e-07|8.5e+12| 5.294769e+12 -1.351390e+12| 0:0:00| chol 2 2 **
**24|0.821|0.581|1.8e-06|1.9e-07|4.3e+12| 2.478233e+12 -7.262154e+11| 0:0:00| chol 2 2 **
**25|0.752|0.900|4.4e-07|2.3e-08|1.4e+12| 1.062699e+12 -1.461507e+11| 0:0:00| chol 1 2 **
**26|0.823|0.824|7.8e-08|6.1e-09|4.6e+11| 3.298022e+11 -5.189739e+10| 0:0:00| chol 1 1 **
**27|0.805|0.886|1.5e-08|1.4e-09|1.4e+11| 1.016861e+11 -1.735180e+10| 0:0:00| chol 2 1 **
**28|0.742|0.798|3.9e-09|6.0e-10|7.0e+10| 4.613019e+10 -1.151663e+10| 0:0:00| chol 1 1 **
**29|0.851|0.902|5.9e-10|1.3e-10|1.7e+10| 7.689480e+09 -6.724827e+09| 0:0:00| chol 1 1 **
**30|0.752|0.757|1.5e-10|6.3e-11|9.3e+09| 1.421840e+09 -6.164050e+09| 0:0:00| chol 1 2 **
**31|0.821|0.906|2.6e-11|1.4e-11|2.7e+09|-3.215742e+09 -5.501752e+09| 0:0:00| chol 2 1 **
**32|0.762|0.759|8.1e-12|6.8e-12|1.4e+09|-4.305865e+09 -5.403108e+09| 0:0:00| chol 2 2 **
**33|0.816|0.896|5.0e-12|1.6e-12|4.1e+08|-4.964496e+09 -5.306673e+09| 0:0:00| chol 2 1 **
34|0.756|0.776|9.1e-12|7.9e-13|2.1e+08|-5.118291e+09 -5.290862e+09| 0:0:00| chol 2 2 **
35|0.821|0.920|6.8e-12|2.0e-13|6.3e+07|-5.220671e+09 -5.275235e+09| 0:0:00| chol 2 2 **
36|0.830|0.947|2.2e-12|7.3e-14|2.1e+07|-5.252419e+09 -5.271477e+09| 0:0:00| chol 1 2 **
37|0.857|1.000|5.0e-12|2.1e-14|4.8e+06|-5.264923e+09 -5.269312e+09| 0:0:00| chol 2 2 **
38|0.820|0.977|2.5e-12|9.1e-15|1.4e+06|-5.267591e+09 -5.268876e+09| 0:0:00| chol 2 2 **
39|0.677|0.916|2.2e-12|6.2e-15|8.1e+05|-5.268040e+09 -5.268764e+09| 0:0:00| chol 1 1 **
40|0.727|0.971|2.5e-12|3.8e-15|4.8e+05|-5.268284e+09 -5.268718e+09| 0:0:00| chol 1 1 **
41|0.732|0.987|2.3e-12|1.7e-15|2.6e+05|-5.268447e+09 -5.268682e+09| 0:0:00| chol 1 1 **
42|0.876|0.985|1.5e-12|5.5e-16|8.0e+04|-5.268581e+09 -5.268653e+09| 0:0:00| chol 2 1 **
43|0.639|1.000|2.3e-12|8.1e-15|5.0e+04|-5.268602e+09 -5.268648e+09| 0:0:00| chol 1 1 **
44|0.873|0.987|4.0e-12|1.3e-16|1.5e+04|-5.268629e+09 -5.268642e+09| 0:0:00| chol 2 1 **
45|0.738|0.995|5.4e-13|9.9e-17|6.5e+03|-5.268634e+09 -5.268640e+09| 0:0:00| chol 2 2 **
46|0.841|0.989|1.2e-12|1.8e-16|2.1e+03|-5.268637e+09 -5.268639e+09| 0:0:00| chol 2 2 **
47|0.678|1.000|4.3e-14|2.0e-16|1.2e+03|-5.268638e+09 -5.268639e+09| 0:0:00|# chol 2 1 **
48|1.000|0.979|2.3e-12|1.2e-18|1.6e+02|-5.268639e+09 -5.268639e+09| 0:0:00| chol 1 1 **
49|0.903|0.978|1.6e-12|1.3e-16|4.7e+01|-5.268639e+09 -5.268639e+09| 0:0:00|
** stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
** number of iterations = 49
** primal objective value = -5.26863859e+09
** dual objective value = -5.26863863e+09
** gap := trace(XZ) = 4.71e+01
** relative gap = 4.47e-09
** actual relative gap = 4.02e-09
** rel. primal infeas (scaled problem) = 1.60e-12
** rel. dual " " " = 1.27e-16
** rel. primal infeas (unscaled problem) = 0.00e+00
** rel. dual " " " = 0.00e+00
** norm(X), norm(y), norm(Z) = 4.6e+12, 1.7e+19, 1.7e+19
** norm(A), norm(b), norm© = 1.6e+04, 2.8e+07, 2.1e+07
** Total CPU time (secs) = 0.23 **
** CPU time per iteration = 0.00 **
** termination code = 0
** DIMACS: 3.8e-12 0.0e+00 2.2e-16 0.0e+00 4.0e-09 4.5e-09
-------------------------------------------------------------------

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +5.15589e+09

K>>

Thank for your time and help!

Christ · July 8, 2019, 10:07am

It is weird that inequation (44) is obviously a convex constraint. And if the initialization is not right, at least the resulting CVX status shall present “Infeasible”.

We have tried Mosek the other day. But found that your CVQUAD’s Pade Approximant works well in our previous problem and the previous problem is also a part of the whole Matlab code. So I am trying to solve the previous problem and the new one with the same solver.

Mark_L_Stone · July 8, 2019, 10:15am

Convexity does not imply numerically “nice”

I suggest you concentrate in improving the numerical formulation. I’d be surprised if SDPT3 worked better than Mosek. And even if SDPT3 reported success while Mosek failed, it could be that SDPT3 erroneously declared success.

Just to be clear, I am suggesting using Gurobi or Mosek with CVXQUAD, not instead of it.

But, it’s your problem, so do what you want.

Christ · July 8, 2019, 10:32am

Get it!
Thanks for the illustration!

Christ · July 8, 2019, 11:49am

Dear Sir:

We combined Mosek with CVXQUAD, as can be seen below.

The question is： does Mosek support the following two rules in CVXQUAD?

Replace
log(cvx_expression)
with
-rel_entr(1,cvx_expresion)

Replace
exp(cvx_expression)
with
z
and add
variable z % this line must be before z is used
cvx_expression + rel_entr(1,z) <= 0

The matlab just output the following information. We have get the licence and install Mosek.
I believe Mosek is called, as can be seen in the following bold expressions.

> =====================================
> =====================================
> Using Pade approximation for exponential
> cone with parameters m=3, k=3
> =====================================
> 
**> Calling Mosek ![](file:///C:\Users\31297\AppData\Roaming\Tencent\QQ\Temp\%W@GJ$ACOF(TYDYECOKVDYB.png)8.0.0.60: 233 variables, 91 equality constraints**
**> For improved efficiency, Mosek is solving the dual problem.**
> ------------------------------------------------------------
> NOTE: custom settings have been set for this solver.
> ------------------------------------------------------------
> *** Error(1200): param.rmdepconstr
> Return code - 1200 [MSK_RES_ERR_IN_ARGUMENT] [A function argument is incorrect.]
> ------------------------------------------------------------
> Status: Error
> Optimal value (cvx_optval): NaN
> 
> *One*  or  *more output arguments not assigned*  during  *call*  to " *mosekopt* ".
> 
> Error cvx_mosek
> 
> Error cvx_run_solver (line 50)
> [ varargout{1:nargout} ] = sfunc( inputs{:} );

Mark_L_Stone · July 8, 2019, 11:59am

Per your previous program using SDPT3, you issued the command cvx_solver_settings('rmdepconstr',1)
outside of cvx_begin … cvx_end . Therefore, it has effect for the rest of the MATLAB session, So the parameter setting of `rmdepconstr’ was in effect for the call to Mosek, and Mosek rejected it as an invalid parameter. I suggest you start a new MATLAB session.

Christ · July 8, 2019, 12:23pm

Dear Sir:
The above custom settings problem is solved.
With Mosek, Matlab gives us more infomation. As can be seen below:

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

Calling Mosek 8.0.0.60: 234 variables, 91 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 8.0.0.60 (Build date: 2017-3-1 13:09:33)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

MOSEK warning 52: A numerically large lower bound value 2.8e+011 is specified for constraint ‘’ (26).
MOSEK warning 53: A numerically large upper bound value 2.8e+011 is specified for constraint ‘’ (26).
MOSEK warning 52: A numerically large lower bound value 2.2e+011 is specified for constraint ‘’ (41).
MOSEK warning 53: A numerically large upper bound value 2.2e+011 is specified for constraint ‘’ (41).
MOSEK warning 52: A numerically large lower bound value 2.6e+011 is specified for constraint ‘’ (56).
MOSEK warning 53: A numerically large upper bound value 2.6e+011 is specified for constraint ‘’ (56).
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 91
Cones : 69
Scalar variables : 234
Matrix variables : 0
Integer variables : 0

Optimizer started.
Conic interior-point optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 9
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.02
Lin. dep. - number : 0
Presolve terminated. Time: 0.02
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 60
Optimizer - Cones : 69
Optimizer - Scalar variables : 214 conic : 207
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 146 after factor : 151
Factor - dense dim. : 0 flops : 1.63e+003
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.1e+009 9.0e+005 2.9e+005 0.00e+000 -4.640991451e+009 6.197640283e+007 1.0e+000 0.02
1 2.1e+008 1.7e+005 2.4e+004 -1.00e+000 8.697563878e+010 9.165826398e+010 1.9e-001 0.05
2 3.6e+007 3.0e+004 1.7e+003 -1.00e+000 7.065930455e+011 7.112798274e+011 3.3e-002 0.05
3 8.0e+006 6.7e+003 1.8e+002 -1.00e+000 3.312483471e+012 3.317171293e+012 7.4e-003 0.05
Interior-point optimizer terminated. Time: 0.05.

MOSEK PRIMAL INFEASIBILITY REPORT.

Problem status: The problem is primal infeasible

Optimizer terminated. Time: 0.06

Interior-point solution summary
Problem status : PRIMAL_INFEASIBLE
Solution status : PRIMAL_INFEASIBLE_CER
Dual. obj: 2.4692108290e+010 nrm: 1e+012 Viol. con: 0e+000 var: 7e-001 cones: 0e+000
Optimizer summary
Optimizer - time: 0.06
Interior-point - iterations : 3 time: 0.05
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Status: Unbounded
Optimal value (cvx_optval): -Inf

The below statement:
MOSEK warning 52: A numerically large lower bound value 2.8e+011 is specified for constraint ‘’ (26).
implies that the problem scale still exists???
Besides this, is there any other problem that is revealed from ?

The Optimization problem is convex. But sometimes CVX failed to find the optimal solution

Successive approximation method to be employed. For improved efficiency, SDPT3 is solving the dual problem. SDPT3 will be called several times to refine the solution. Original size: 24 variables, 8 equality constraints 4 exponentials add 32 variables, 20 equality constraints

Cones | Errors | Mov/Act | Centering Exp cone Poly cone | Status --------±--------------------------------±-------- 0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed 0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed 0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed

===========================================

Using Pade approximation for exponential cone with parameters m=3, k=3

===================================== Using Pade approximation for exponential cone with parameters m=3, k=3

===================================== Using Pade approximation for exponential cone with parameters m=3, k=3

===================================== Using Pade approximation for exponential cone with parameters m=3, k=3

===================================== Using Pade approximation for exponential cone with parameters m=3, k=3

Calling SDPT3 4.0: 108 variables, 40 equality constraints For improved efficiency, SDPT3 is solving the dual problem.

version predcorr gam expon scale_data HKM 1 0.000 1 0 it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

number of iterations = 18 Total CPU time (secs) = 0.33 CPU time per iteration = 0.02 termination code = 3 DIMACS: 3.8e+00 0.0e+00 3.0e+00 0.0e+00 -1.0e+00 3.0e-03

Using Pade approximation for exponential cone with parameters m=3, k=3

===================================== Using Pade approximation for exponential cone with parameters m=3, k=3

===================================== Using Pade approximation for exponential cone with parameters m=3, k=3

===================================== Using Pade approximation for exponential cone with parameters m=3, k=3

===================================== Using Pade approximation for exponential cone with parameters m=3, k=3

Calling SDPT3 4.0: 108 variables, 40 equality constraints For improved efficiency, SDPT3 is solving the dual problem.

===================================== Using Pade approximation for exponential cone with parameters m=3, k=3

Calling Mosek 8.0.0.60: 234 variables, 91 equality constraints For improved efficiency, Mosek is solving the dual problem.

Successive approximation method to be employed.
For improved efficiency, SDPT3 is solving the dual problem.
SDPT3 will be called several times to refine the solution.
Original size: 24 variables, 8 equality constraints
4 exponentials add 32 variables, 20 equality constraints

Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed

Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

Calling SDPT3 4.0: 108 variables, 40 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.

version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

number of iterations = 18
Total CPU time (secs) = 0.33
CPU time per iteration = 0.02
termination code = 3
DIMACS: 3.8e+00 0.0e+00 3.0e+00 0.0e+00 -1.0e+00 3.0e-03

Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

Calling SDPT3 4.0: 108 variables, 40 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

Calling Mosek 8.0.0.60: 234 variables, 91 equality constraints
For improved efficiency, Mosek is solving the dual problem.