My MATLAB code is as follows:
Nt, M, and SINR are constants.
However, when SINR > 1e-10, the derived lambda(K) are NaN.
Is this because that there is no feasible solution?
Nt, M, and SINR are constants.
However, when SINR > 1e-10, the derived lambda(K) are NaN.
Is this because that there is no feasible solution?
You haven’t provided a reproducible example, i.e., with input data, which would allow us to investigate.
I recommend you remove the quiet option, so that the solver output and the Status and Optimal value returned by CVX will be displayed. My guess is that when SINR > 1e-10, your problem is infeasible and you will the see the following:
Status: Infeasible Optimal value (cvx_optval): +Inf
In such case, the optimization variables would all be NaN
After you have CVX and the optimization problem solution running smoothly, then you can consider using the quiet option.
I have tried and you are right.
the MATLAB pointed out
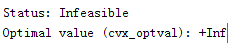
In that case, how do I solve the optimization problem?
Does it mean that it cannot be solved?
The optimization problem as provided can not be solved. However, if you eliminate or modify certain constraints, it would be feasible (certainly if you eliminate all constraints).
Of course, you can modify your “constants” (input data).
Something you can try is to remove one or more semidefinite constraints, and replace the objective with maximize(lambda_min(X)), where X is one of the matrices you are constraining to be senidefinite. Or perhaps, the sum of lambda_min of several of the semidefintie-constrained matrices. You can see how close lambda_min is coming to zero. If (the optimal) lambda_min is negative of large magnitude, the matrix is not close to being semidefinite.
1 Like
Okay, thank you very much.
I will have a try.