SOCP reformulation

1

I have the following SOCP
55 PM
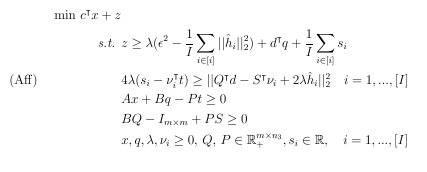
with code in matlab
function [optval,rtime]=TwoStageAffine(n,m,N,c,d,epsilon,A,B,h,S,t)
o=length(t);
M= (1/N)*sum(sum(h.^2,2));
tic
cvx_begin quiet
variable x(n) nonnegative;
variable Q(n,m);
variable q(n) nonnegative;
variable z(1);
variable s(N);
variable l(1) nonnegative;
variable v(o,N) nonnegative;
variable P(m,o) nonnegative;
variable W(2,2,N);

minimize(c.'*x+z);
    subject to
        z>= l*(epsilon^2-M)+d.'*q+(1/N)*sum(s);
        A*x+B*q-P*t>=0;
        B*Q-eye(m)+P*S>=0;
        for i=1:N
            expression WW1(1);
            expression WW2(1);
            WW1==4*l*(s(i)-v(:,i).'*t);
            WW2==norm(Q.'*d-S.'*v(:,i)+2*l*h(:,i));
            W(:,:,i)==[WW1,WW2;WW2,1];
            W(:,:,i)==semidefinite(2,2);
        end

cvx_end
I’m getting the error: “Disciplined convex programming error: Invalid quadratic form(s): not a square.”
I know the issue is on the norm constraint and the fact that \lamba (variable) is multiplied by both s_i and v_i, both variables. I have it running using gurobi in pyhton but for simulations reasons it wil be more convenient to have it in matlab. Yet I still don’t know who to plug it in to CVX properly.
I will appreciated any advice

2

I think you may want to change your norm constraint so that it conforms to the ruleset of DCP. Also, this will remove the semidefinite constraint and replace it with a second-order cone constraint, as follows:

(please check the validity before applying it):

WW1=sqrt(2)* norm( [ l+s(i); l+v(:,i).‘t]);
WW2=norm([ Q.d-S.v(:,i)+2lh(:,i); sqrt(2) (l-s(i)); sqrt(2)*(l-v(:,i).’*t)]);
WW2<=WW1; % constraint