Hi guys,
I am having an issue writing the Schur complement in CVX that keeps telling me “Disciplined convex programming error”. Here is my problem, I have the following matrix [X x; x’ 1] which is positive semidefinite. Note that X is a K \times K matrix and x column vector of size K. If I write
[[X x];[x’ 1]] == semidefinite(K+1), it works fine. For some reasons, I need to write it as
two constraints, i.e. X positive semidefinite and X-xx’ positive semidefinite. So when I write
X== semidefinite(K) and X-xx’ == semidefinite(K)
CVX says that “Disciplined convex programming error”. I am almost certain that the problem is with the product "xx’ ". Does someone have a solution to write "xx’ " in CVX?
You simply cannot. You will have to use the first approach. Why do you think you “need” to write it as two equations.
@mcg I am solving an optimization problem using SDR approach. I have provided an optimality condition (which permits to have a rank one solution) where the theoretical analysis was mainly based on the rank of the Lagrangian multipliers associated with the constraint X-x*x’. So I need to see if empirically, it is really true.
Thanks for replying anyway.
Cheers,
That doesn’t explain why you need the two constraints together. The first one is exactly equivalent to the two-constraint form, only it is actually convex and in a form CVX can handle.
Hi, can you help me?
I have a problem. when i write the picture to matlab, CVX says:
‘‘Disciplined convex programming error:
Invalid constraint: {complex affine} >= {real affine}’’
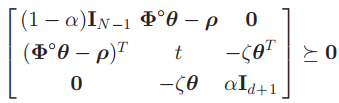
variable teta(3)
variable t(1)
variable alfa(1)
minimize( t )
subject to
[eye(2) [teta(1); teta(2)];[teta(1); teta(2)]' teta(3)]>=zeros(3,3);
[(1-alfa)*eye(length(sx)-1) (phi*teta-Rho) zeros(9,3) ; ...
(phi*teta-Rho)' t -kesi*teta' ; ...
zeros(3,9) -kesi*teta alfa*eye(3) ]>=zeros(13,13);
I think the constraint is quadratic and no affine. what your idea?
Per the error message, your constraint is affine, not quadratic, and as must be the case presuming you have shown all the variable declarations.
My guess: one or more of the MATLAB variables (input data) are complex and you dud not specify sdp mode, i.e.,cvx_begin sdp
Use the sdp mode, and you can make the right-hand side 0, but think it is o.k. as is. Without sdp mode, the constraint is interpreted element-wise, hence the error message if there is complex data on the left-hand side.
Mr Mark, Thanks for your reply. cvx_begin sdp was correct and variable was complex.