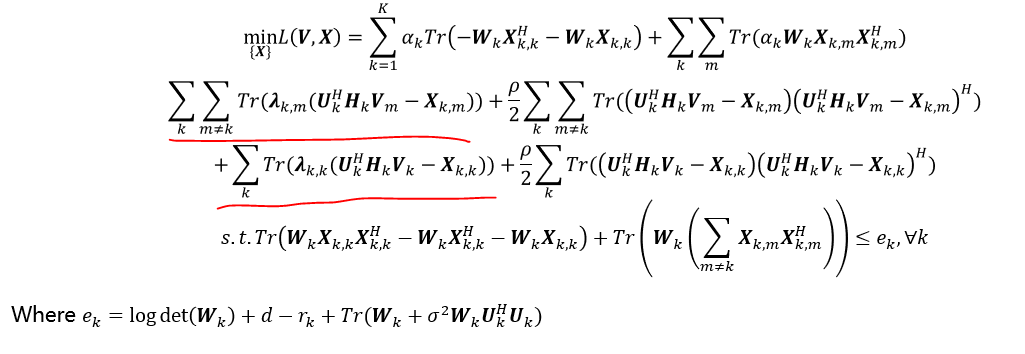Question about the Illegal operation: {complex affine} + {convex}

1

image
image1025×354 20 KB

cvx_clear
cvx_begin quiet
variable x_hat(d,d,K,K) complex
expression obj(1)
expression cons(K)

        for k = 1:K
            obj = obj - real(weights(k) * trace(W(:,:,k) * x_hat(:, :, k, k)' + W(:,:,k) * x_hat(:, :, k, k)));
            for m = 1:K
                obj = obj + weights(k) * square_pos(norm(sqrtm(W(:,:,k))*x_hat(:,:,k,m),'fro'));

                % underlined part
                obj = obj + real(trace(lamda(:, :, k, m)*(U(:,:,k)'*H(:,:,k)*V(:,:,m) - x_hat(:, :, k, m))));

                obj = obj + 0.5 * rho * square_pos(norm(U(:,:,k)'*H(:,:,k)*V(:,:,m) - x_hat(:, :, k, m), 'fro'));
            end
        end

        for k = 1:K
            cons(k) = cons(k) - real(trace(W(:,:,k) * x_hat(:, :, k, k)' + W(:,:,k) * x_hat(:, :, k, k)));
            for m = 1:K
                cons(k) = cons(k) + square_pos(norm(sqrtm(W(:,:,k))*x_hat(:,:,k,m),'fro'));
            end
        end

        minimize (obj)

        subject to 
            for k = 1:K
                cons(k) <= e(k);
            end

    cvx_end
    X(:, :, :, :) = x_hat(:, :, :, :);

The convex problem is shown in the figure, where W is a positive semidefinite hermitian matrix . And i am trying to solve it with CVX. However, the trace of the underlined part is a complex value. The error occurred when i just used trace(), so i changed the code with real(trace())

(obj = obj + real(trace(lamda(:, :, k, m)*(U(:,:,k)’*H(:,:,k)*V(:,:,m) - x_hat(:, :, k, m))));),

but actually it is a complex value. I did not get the results I want, and I think there might be something wrong here. Or is there anything wrong with my code?

Anyone can help me to solve this problem ? thank you so much :grinning:

2

Is there any theoretical reason that term should be real (even if computed in exact arithmetic)? Does it somehow combine with other terms to net out to real? How is that addressed in whatever paper or book the formulation is from?

4

Thanks for your reply. Actually, it is not necessary to be real, But it can be prove that other terms are real. For example, Tr(WXX’) = Tr(X’ W X) and X’ W X is a hermitian matrix, so the imag part of Tr(W X X’) is 0.
To satisfy the rule of CVX, i wrote Tr(WXX’) as square_pos(norm(sqrtm(W(:,:,k))x_hat(:,:,k,m),‘fro’)), which is a real value.
But trace(lamda(:, :, k, m)(U(:,:,k)’*H(:,:,k)*V(:,:,m) - x_hat(:, :, k, m))) is a complex value, and the error {complex affine} + {convex} occurred. In order to make CVX work, i toke the real part of trace.
I know it is something wrong with this procedure, but i have no idea how to deal with this problem properly.
I will be very appreciated if you could give me some suggestions.

5

My suggestion is to go to the source of the problem, and figure it out, and if you can’t figure it out, ask the authors. Objective functions in optimization (convex or non-convex) must evaluate to real (scalar). “Yours” does not; therefore it is not a convex optimization problem.

Perhaps it is as simple as a missing Re(...) in the depicted formulation. or maybe there’s some other explanation. Or maybe the formulation doesn’t make any sense. That is not for this forum to determine.

6

Thanks for your help, i will check the formulation again.