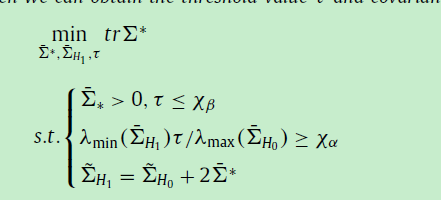
Can I use the CVX tool to slover this problem? Thank you!
The objective function is linear, but the left side of the second constraint is not concave, so this problem is not convex. You have to firstly transform this probem into a convex one equivalently.
I’ll presume the relevant matrices are symmetric positive semidefinite, and that \tau also has a lower bound of zero (or greater) although I don’t see that explicitly stated in what is shown.
You can multiply the constraint on the 2nd line of constraints by \lambda_{max}. But the product term between \lambda_{min} and \tau is non-convex and will not be allowed by CVX. You could deal with that by not declaring \tau as a CVX variable, and instead, solve a separate CVX problem for each fixed value of \tau over a grid of its possible values. Then choose the solution with the best objective value from among these problems.
Actually, I believe that constraint is quasi-convex, so can be handled by using the bisection algorithm in section 4.2.5 “Quasiconvex optimization” of " Convex Optimization" by Boyd and Vandenberghe https://web.stanford.edu/~boyd/cvxbook/
I get. Thank you very much!
I get. Thank you very much!