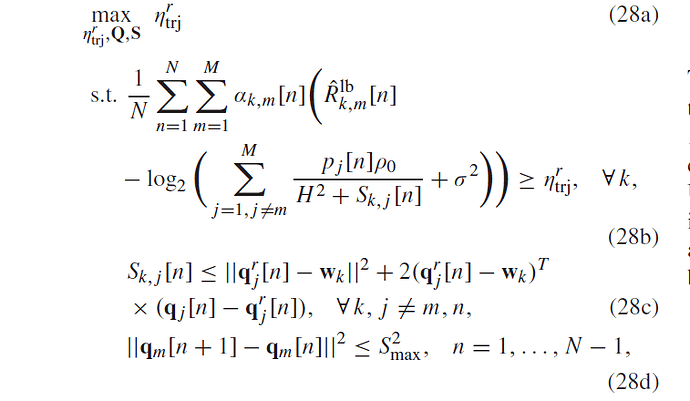In one of my work, I am trying to implement the above function on simple on constraints the variable x_{i}. The problem is that inv_pos returns positive convex function and the domain of log needs concave. Could you please let me know how can I implement this using CVX?
This is handled in a CVX-compatible fashion (make use of CVX’s log_sum_exp) in Section 5.2.7 “Log-sum-inv” of Mosek Modeling Cookbook 3.1
Dear Mark,
Thank you so much for your prompt response. Indeed, I just simplified the problem that I actually want to implement, attached.
My understanding of your previous response is that I should change the variables S_{k, j} and add some new constraints on optimization. Am I correct?
You need to adapt the formulation in the link to handle your problem. You will need to introduce new variables and constraints, which will take a more comp0licated form than in the simpler problem in the link. I’ll leave that to you.
Thank you so much for your efforts, much appreciated.
The last think that I wonder to check with you is that do you think if I implement another optimization inside this optimization for S_{k,j} using the link you provided then put the solution of the new optimization into the main optimization, would it work?
Best,
Iman
It should “work” if you do it correctly, which will of course require the input data (parameters) to be of the correct sign, which I assumed (otherwise the constraint will not be convex). There is not a “separate” optimization inside another. You need to add variables and constraints to your overall problem/
Given use of log)sum_exp and exp, after you verify you have the initial model accepted by CVX, you follow the advice at CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions
I suggest you start with a simplified problem, get that working, then attempt the problem you really want to solve. Fort instance, start with the simplified constraint in the link, then increase the complexity to the problem you really want to solve.
Dear Mark,
Thanks again for your promising responses. I will indeed follow your instructions.
Best,
Iman