Hi all,
I am a newbie to CVX tool and trying to implement a problem (Snapshot Attached). I have tried many ways but unable to find the solution. I want to solve it as a Linear Program.
lpi_hat =[5 0;0 5];
lpv_hat=[-1 0 -1 0 -1 0 -1 0 -1 0;0 -1 0 -1 0 -1 0 -1 0 -1];
x_v= [1;4;3;4;5;2;3;1;1;1];
x_j=[2;5];
d=[4;4];
cvx_begin
variable x_p(2)
minimize (-lpi_hat.*x_p-lpv_hat.*x_v)
subject to
(x_p)-(x_j)<=d
cvx_end
I am continuously facing a problem like
"Error using .* (line 46)
Matrix dimensions must agree.
Error in CVX_Examplr (line 11)
minimize (-lpi_hat.*x_p-lpv_hat.*x_v)"
I will be quite thankful if someone can help me in this regard.
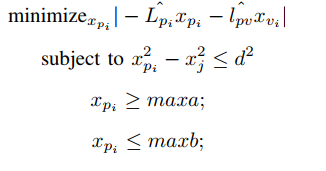
You should not be using .*
Perhaps you want
minimize (norm(-lpi_hat*x_p-lpv_hat*x_v,1))
or
minimize (norm(-lpi_hat*x_p-lpv_hat*x_v,inf))
Using either of these, your program will run without error message. However, You have not correctly implemented the constraint in the image. I believe you want
x_p.^2 - x_j.^2 < = d^2
However, that is a convex quadratic constraint, not a linear constraint. It can be solved as is in CVX. . However, it can instead be transformed into two linear (affine) constraints, which when using the one norm or infinity norm in the objective function, will result in a Linear Program.
x_p <= sqrt(x_j.^2 + d^2)
- x_p <= sqrt(x_j.^2 + d^2)
And you forgot to include the constraint
maxa <= x_p <= maxb
So the complete program is
cvx_begin
variable x_p(2)
minimize (norm(-lpi_hat*x_p-lpv_hat*x_v,1))
x_p <= sqrt(x_j.^2 + d^2)
- x_p <= sqrt(x_j.^2 + d^2)
maxa <= x_p <= maxb
cvx_end
Or perhaps you want
minimize (norm(-lpi_hat*x_p-lpv_hat*x_v,inf))
for the objective.
Edit: I changed d to d^2, so as to match your Snapshot.
1 Like
I am highly thankful for the response. The code perfectly worked for me.