hi , my code is
clear all
close all
ebn0=10;m=21;B=40;np=1;pt=10;
ebd= 10log10((Bpt)/m) ;
eb=10^(.1ebd);
ebn0ad=10^(.1ebn0);
n0=(eb/ebn0ad);
cvx_solver SDPT3
cvx_begin
alpha=[.75;.85;1.3];
y=3*(alpha.^2);
variables t p(3)
dual variables landa1 landa2 landa3 miu z
minimize(t)
subject to
landa1:(p(1) * inv_pos(y(1) * (eb/n0)))+(inv_pos(y(1) * (eb/n0)))+(inv_pos(m * y(1) * (eb/n0)))+(inv_pos(m * p(1). * y(1) * (eb/n0)))+((B * p(1). * inv_pos(2 * (y(1).^2) * ((eb/n0)^2))))+(B * inv_pos(m*(y(1).^2) * ((eb/n0)^2)))+(B * inv_pos(2*(m^2)*p(1). * (y(1).^2) * ((eb/n0)^2)))<=t
landa2:(p(3) * inv_pos(y(2) * (eb/n0)))+(inv_pos(y(2) * (eb/n0)))+(inv_pos(m * y(2) * (eb/n0)))+(inv_pos(m * p(2). * y(2) * (eb/n0)))+((B * p(2). * inv_pos(2 * (y(2).^2) * ((eb/n0)^2))))+(B * inv_pos(m*(y(2).^2) * ((eb/n0)^2)))+(B * inv_pos(2*(m^2)*p(2). * (y(2).^2) * ((eb/n0)^2)))<=t
landa3:(p(3) * inv_pos(y(3) * (eb/n0)))+(inv_pos(y(3) * (eb/n0)))+(inv_pos(m * y(3) * (eb/n0)))+(inv_pos(m * p(3). * y(3) * (eb/n0)))+((B * p(3). * inv_pos(2 * (y(3).^2) * ((eb/n0)^2))))+(B * inv_pos(m*(y(3).^2) * ((eb/n0)^2)))+(B * inv_pos(2*(m^2)*p(3). * (y(3).^2) * ((eb/n0)^2)))<=t
miu:sum§<=((pt-G)/21);
z:p>[0; 0; 0];
cvx_end
miu = 1.326713680213978e-09 is within solver tolerance of being zero, so you can think of it as being zero.
thanks dear mark. about lambda, consider the conceptual case with G=3, obtained values meet the optimality condition “sum(lambda)=1”, but regarding to the slackness condition " sum(lambda)*(pi(g)-t)=0" i expect " pi(g)=t * " for all g={1,2,3}, while CVX gives this for g=1 only and “pi(2)<t *”,"pi(3)<t * ". if we suppose that cvx consider the worst case and the two other pi(1),pi(2) are smaller than t *, regarding to the cost function, cvx calculated one of the p * (g)'s as the optimal solution. my question is that :are the two other p(2) , p(3) optimal? if no , how are calculated by CVX? regards. if are optimal, why not consider the worst case for them? regards
I don’t understand what you are saying.
What does the solver output show? What does CVX provide as the solution status? If they are reporting an optimal solution has been found, then the solution is optimal within the specified tolerance. But due to solver tolerance, complementary slackness conditions may not be satisfied exactly, but must be satisfied to within the tolerance. You can also try specifying cvx_solver sedumi , or another solver if available, and see what solution it provides.
i try to summarize the question.
my variables are p1, p2, p3, t.
i thik it dont have relation with tolerance because regarding to CVX solution, sum(lambda)=1 and its OK. thus, due to slackness condition of the first constraint" sum(lambda)*(pi(g)-t)=0" ,we must have “pi(g)=t " or “pi(g)= +0.108065” for all g={1,2,3}.
but when i put the CVX solutions ( p1, p2 , p3 ) in the cost function, i obtain “pi(1)= +0.108065” only and ,“pi(2)< +0.108065”,“pi(3)< +0.108065”. this result is unexpected for me because regarding to above mentioned slackness condition we must have"pi(1)=+0.108065" ,"pi(2)=+0.108065”,“pi(3)=+0.108065”.
%%%%%%%%%%%%%%%%%%%%%%%%%%%% solver output:
Calling SeDuMi 1.34: 25 variables, 10 equality constraints
For improved efficiency, SeDuMi is solving the dual problem.
SeDuMi 1.34 (beta) by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, Adaptive Step-Differentiation, theta = 0.250, beta = 0.500
eqs m = 10, order n = 20, dim = 26, blocks = 7
nnz(A) = 45 + 0, nnz(ADA) = 52, nnz(L) = 31
it : by gap delta rate t/tP t/tD* feas cg cg prec
0 : 3.03E+05 0.000
1 : 9.91E-04 2.24E+04 0.000 0.0739 0.9900 0.9900 -0.54 1 1 1.5E+03
2 : -1.10E+01 6.08E+03 0.000 0.2711 0.9000 0.9000 0.83 1 1 4.6E+02
3 : -1.96E+01 1.61E+03 0.000 0.2645 0.9000 0.9000 0.24 1 1 2.3E+02
4 : -2.21E+01 7.49E+02 0.000 0.4656 0.9000 0.9000 0.10 1 1 1.5E+02
5 : -1.77E+01 4.93E+02 0.000 0.6589 0.9000 0.9000 0.36 1 1 1.1E+02
6 : -1.40E+01 2.44E+02 0.027 0.4944 0.9000 0.9000 0.39 1 1 6.8E+01
7 : -1.07E+01 1.14E+02 0.122 0.4672 0.9000 0.9000 0.33 1 1 4.2E+01
8 : -7.70E+00 3.88E+01 0.000 0.3407 0.9000 0.9000 0.46 1 1 1.8E+01
9 : -4.89E+00 9.76E+00 0.000 0.2515 0.9000 0.9000 0.32 1 1 7.1E+00
10 : -3.21E+00 2.87E+00 0.000 0.2943 0.9000 0.9000 0.44 1 1 2.9E+00
11 : -2.22E+00 9.48E-01 0.000 0.3301 0.9000 0.9000 0.44 1 1 1.3E+00
12 : -1.53E+00 3.31E-01 0.000 0.3492 0.9000 0.9000 0.42 1 1 6.7E-01
13 : -1.11E+00 1.20E-01 0.000 0.3614 0.9000 0.9000 0.52 1 1 3.2E-01
14 : -7.60E-01 3.82E-02 0.000 0.3195 0.9000 0.9000 0.41 1 1 1.5E-01
15 : -5.57E-01 1.32E-02 0.000 0.3464 0.9000 0.9000 0.48 1 1 7.1E-02
16 : -3.81E-01 3.88E-03 0.000 0.2933 0.9000 0.9000 0.38 1 1 3.3E-02
17 : -2.82E-01 1.30E-03 0.000 0.3340 0.9000 0.9000 0.45 1 1 1.5E-02
18 : -1.96E-01 3.40E-04 0.000 0.2620 0.9000 0.9000 0.37 1 1 6.3E-03
19 : -1.50E-01 1.01E-04 0.000 0.2973 0.9000 0.9000 0.46 1 1 2.6E-03
20 : -1.26E-01 3.70E-05 0.000 0.3662 0.9000 0.9000 0.45 1 1 1.3E-03
21 : -1.13E-01 1.24E-05 0.000 0.3346 0.9000 0.8576 0.58 1 1 5.4E-04
22 : -1.10E-01 4.35E-06 0.000 0.3514 0.9000 0.9000 0.73 1 1 2.1E-04
23 : -1.08E-01 1.40E-07 0.000 0.0322 0.9900 0.9900 0.93 1 1 7.1E-06
24 : -1.08E-01 6.74E-10 0.000 0.0048 0.9990 0.9990 0.99 2 2 3.4E-08
25 : -1.08E-01 4.52E-12 0.260 0.0067 0.9990 0.9990 1.00 2 2 2.3E-10
iter seconds digits cx by
25 1.3 Inf -1.0806548480e-01 -1.0806548397e-01
|Ax-b| = 2.6e-10, [Ay-c]_+ = 0.0E+00, |x|= 2.8e+01, |y|= 3.8e+04
Detailed timing (sec)
Pre IPM Post
3.690E-01 1.023E+00 8.800E-02
Max-norms: ||b||=1, ||c|| = 2,
Cholesky |add|=0, |skip| = 0, ||L.L|| = 2.62135e+07.
Status: Solved
Optimal value (cvx_optval): +0.108065
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
solution vaues:
t=+0.108065
p
p =
0.151752321454870
0.071750033729841
0.017813553181463
landa1
landa1 =
0.999999855523484
landa2
landa2 =
9.267594913631824e-08
landa3
landa3 =
5.180098250953069e-08
miu
miu =
1.159409863364395e-08
landa2 and landa3 are less than 1e-7 in magnitude, and therefore can be considered to be within tolerance of zero. I.e., for evaluation of complementary slackness, consider them to be zero. Because they are zero, complementary slackness holds for the corresponding constraints. CVX and SDPT3 appear to be functioning properly. That fact that sum(lamba) is within 4e-13 of being 1 does not invalidate what I have written. Please read http://web.cvxr.com/cvx/doc/solver.html#controlling-precision .
if landa2 =0 , landa3=0, regarding to derivative of the lagrangian, p2* and p3* must be zero .it is aan infeasible solution because my last constraint is p_g>0.
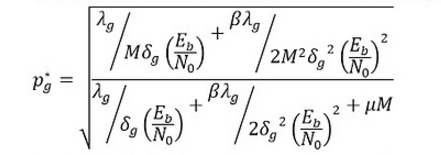
Per http://web.cvxr.com/cvx/doc/dcp.html#strict , strict inequalities are treated as being non-strict. I.e. p > 0 is treated as being p >= 0. Therefore, p = 0 is considered to be feasible (indeed, even a very slightly negative value of p can be considered to be feasible).
I haven’t attempted to verify your analytical solution, and am somewhat confused by your presentation. I think you will find that KKT optimality conditions are within tolerance of being satisfied for the solution returned by CVX/SeDuMi.
the analytical solutions is true. from a theoretically aspect, because the main problem is an epigraph form of a min-max problem( or worst case problem), i think that CVX optimize p1*,t*. as the worst case. therefore, p2, p3 may not be optimal necessarily.from this point of view, this is reasonable that landa2 , landa3 and p2, p3 dont meet the KKT conditions. excuse me sir, i am confuse too.
CVX/SeDuMi or SDPT3 are solving the optimization problem as you have entered it. If the problem you entered is not the correct one relative to what you are trying to do, then that is your responsibility, and CVX and its solvers can be held blameless in such situation. I.e., CVX and its solvers solve the problem from the point of view of what you have entered as your problem.
i think that the code is true and this is clear in my second post. Did you mean that it may not be a feasible solution for the designed problem (for P_T >8)? it’s possible.
As far as I can tell, the solver and CVX returned an optimal, and therefore primal feasible, solution to the problem you entered into CVX. I don’t know whether an optimal solution to the problem you entered into CVX is an optimal, or even primal feasible solution, to whatever min-max problem you really want to solve.
![]() thank you very much
thank you very much