R is a N*N matrix.P = diag p1,p2,p3…,is a diagonal matrix of vector p.The original paper says this probem is a regularized convex optimization problem.
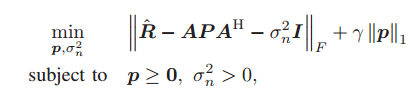
Is everything in the objective function, other than p, P, and \sigma^2_n, input data? If so, declare p and \sigma^2_n (not \sigma_n) to be CVX variables, and you can enter this into CVX essentially as written, using diag(p) for P.
Thank you.i did as what you say.It is useful.And i make a transformation to this formula,then its Status: Infeasible Optimal value (cvx_optval): +Inf.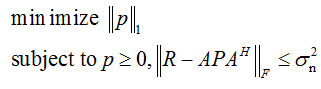
everything in the objective function, other than p, P, is input data.can you teach me?
Your second version is not equivalent to the first version. The first version should be feasible (unless the scaling is so screwed up that a solver misreports it). But th3 2nd version may or may not be feasible depending the input data - with your particular data it apparently is infeasible. If you want to solve the first problem, then enter that.
You say the 2nd version may or may not be feasible depending the input data.Can you give me a specific example of this problem when it wil be feasible or not.The first problem was proposed and solved by others.i must make something new if want to write a paper.Thank you.
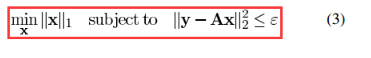
I think my 2nd problem is similar to this one,right?
forgive my poor English
Consider the trivial 1D example having R = 2, A = 0. if \sigma^2 _n < 2, your 2nd formulation is infeasible. if \sigma^2 _n \ge 2, it is feasible.
I am not in the business of doing research for you so that you can write a paper on something new. Perhaps you should spend ,more time learning the basics before trying to write a paper on something new.
This would probably not be a good research paper:
1., I took a formulation I didn’t understand.
2. I modified it to a non-equivalent formulation.
3. The non-equiavalent formulation is lousy.