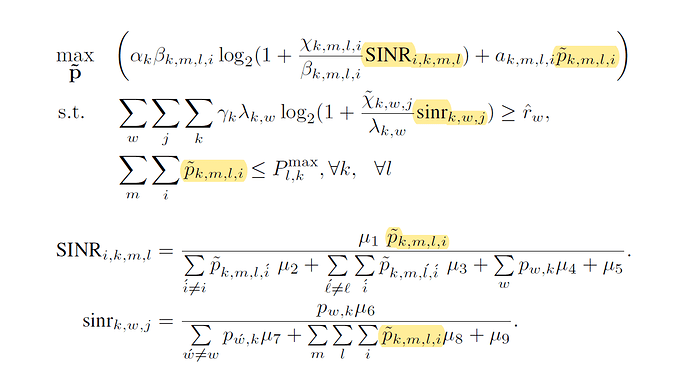Thank you very much for your detailed reply. It helped me a lot.
This is exactly what I wanted to know: “If you have a separate optimization problem for each value of something parameterized by a for loop index variable, then place the for loop outside cvx_begin to cvx_end.”
then as you suggested : “If there is only a single i entering an optimization problem involving p_{i}, and there are n different values of : Declare a scalar variable in CVX, and place for i=1:n outside cvx_begin to cvx_end.”
These are exactly what I am doing and thank for making everything clear.
Here is my issue:
I am trying to solve the following optimization problem without considering any constraints
the variable of interest is ptilda_{k,m,l,i} which is scalar
for k= …
for m = …
for l = …
for i = …
begin_cvx
variable ptilda <=======
calculating the SINR according the formulation
obj = ...
maximize(obj)
end_cvx
end
end
end
end
The cvx gives me an error when want to calculate the first part of the SINR’s denominator.
“Error using cvx/subsref (line 13)
Index in position 1 exceeds array bounds (must not exceed 1)”
The error comes from the fact that I am defining ptilda as a scalar and now it is not able to calculate the function that has nothing to do with this ptilda(k,m,l,i).
Any suggestions for solving this issue would be greatly appreciated.
Thanks