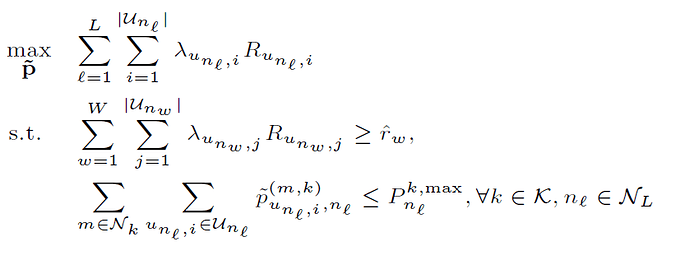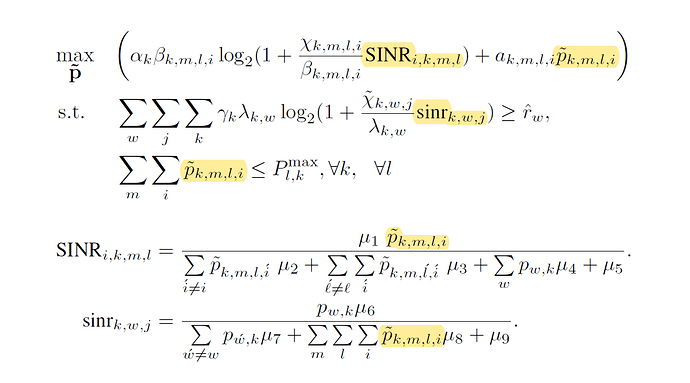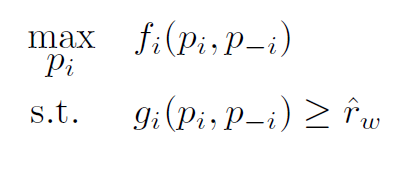How to write this optimization problem in CVX form?

susan · May 6, 2019, 5:59pm

Hey guys,

I have got to solve an optimization problem. The original problem was non-convex (objective function is non-convex in desired variable). I have convexified that and now I want to apply cvx to solve this convex optimization problem.

The variable of interest that I want to find its optimal value is ptilda with the dimension of (I,J,J,K,M). each ptilda is a scalar value which takes values between 0 and 1.
After convexifying the objective function, I have (I,J,K,M) objective function, each correspond to one ptilda.
How should I apply cvx to it? Any help would be greatly appreciated.

Mark_L_Stone · May 6, 2019, 7:11pm

I don’t know what relation this question has to your other question How to write this optimization problem in CVX? . The multiple-level subscripted R in the objective function and the first constraint can be converted to an expression involving rel_entr as shown in my answer to that question, presuming this R is the same as that R, Iif that does not resolve your difficulty, you need to spell out more clearly what is what and where you r difficulty is.

Mark_L_Stone · May 6, 2019, 9:00pm

Also, I recommend you install CVXQUAD and follow the advice at CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions .

susan · May 6, 2019, 9:11pm

Thanks for your reply and the recommendation. Sure, I will install that.
I am trying to make my question more clear before asking that
Thanks again

susan · May 7, 2019, 4:05pm

Hi Mark,

I tried to make my question more clear. Please let me know if it still doesn’t make sense.
The objective function above is nonconvex in “ptilda” where ptilda has the dimensions of (K,M,J,I). I have convexified that and now for a specific (k,m,j,i) the objective function is in the format of
alpha1 * alpha2* log2(1 + alpha3*SINR/alpha2) - alpha4 * ptilda(k,m,j,i)
where SINR is an affine (linear) function of ptilda(k,m,j,i), i.e., SINR = alpha5 * ptilda(k,m,j,i)

I have got KMJ*I of these objective functions, each one correspond to one specific ptilda.
How can I maximize these functions simultaneously (say in a parallel way)? In this case, can I still use rel_entr to convert objective function?

Thank you very much in advance!

Mark_L_Stone · May 7, 2019, 4:26pm

I have no idea what your problem is. How does ptilda relate to R, etc.? Perhaps if you write it all out clearly, with unambiguous relations between the various things made clear. The most important beneficiary of doing so might be you, because then everything will be explicit instead of fuzzy.

Perhaps you could start with a simplified version which gets rid of most of the subscripts and sums. Then write out a complete CVX code, other than perhaps that it might violate some DCP rules. Then maybe forum readers could figure out if/how to fix it up to follow CVX’s DCP rules.

susan · May 7, 2019, 4:28pm

Sure! I will. Thanks again

susan · May 7, 2019, 5:26pm

Here is the problem.
I am not able to get rid of some of the subscripts since they make the original problem non-convex. But I tried to simplify that as much as possible and I have highlighted the variable of interest (or the functions that contain this variable) in the objective function and constraint.
the variable of interest is pitilda with the size of (K,M,J,i) and the following optimization problem is supposed to find the optimal value for ptilda_{k,m,j,l}.
.

My question is, can I use the cvx in the following loops (since I have K * M* J * I objective function now)
for k = …
for m = …
for l = …
for i = …

cvx

end
end
end
end
or there is a better way to implement that?

Is it correct to use rel_entr for converting objective function and constraint in the above problem as follows
objective function = \alpha * \beta * -rel_entr(1,1 + \chi*SINR/\beta) + a ptilda
constraint = sum(\gamma * \lambda * -rel_entr(1,lambda /(lambda +\chi_tilda sinr)))

Thanks in advance

Mark_L_Stone · May 7, 2019, 11:17pm

it appears that SINR and sinr are affine (linear) in the CVX variable ptilda, so use of rel_entr in the objective and constraint should be allowed. But if so, why do you have an error message in Disciplined convex programming error: Cannot perform the operation: {positive constant} ./ {convex}…

You can always use for loops. Your mathematical oprtmization problem formulation is not presented clearly enough for me to figure out whether there is a better way. If I were you, I;d worry about getting a correct model correctly implemented. If you have done that, you can then worry about efficiency improvements. if CVX calls the solver quickly enough, then don;t worry about getting rid of for loops.

You really need to make a clear and self-contained mathematical optimization problem statement. Show the complete code, and if you can, the input data which resulted in whatever error messages you are getting. And please don;t keep starting new threads on the same problem. When you show little bits here and there, and they keep changing, it doesn’t serve anyone’s interest. Maintaining a disciplined approach to your modeling coding, and data management is as or more valuable than mathematical optimization theory knowledge if your goal is to solve and implement solutions to actual problems.

susan · May 8, 2019, 2:15pm

Thank you so much for your reply.
The reason I haven’t shown my code here is in order to create the objective function I need to call several functions and it is kinda mess. I can upload the zip file of my codes if it is allowed here.

Sorry for that. Actually, I made a new thread on another problem. even though the objective function and one of the constraint are the same, but the variable of interest in these two questions are different. One of the problem is originally convex, while this one is originally non-convex. Sorry again if it causes any inconvenience.

susan · May 8, 2019, 5:56pm

Thanks again for your reply.
You stated that “it appears that SINR and sinr are affine (linear) in the CVX variable ptilda”. I think sinr is convex in the CVX variable ptilda. Am I missing something or it is just a typo?

When I run the code I got the error of “Cannot perform the operation: {real affine} ./ {real affine}” in the definition of SINR while it is affine in variable ptilda.

My question is how should I define the CVX variable here? Since I am using 4 for loops over (k,m,l,i) so I defined the cvx variable as an scalar ptilda (inside these loops-- at each round and for a specific k,m, l, i I am optimizing one ptilda(k,m,i,l)) but I got error. Then I defined the CVX variable as ptilda(K,M,I,L) and now I am getting this “{real affine} ./ {real affine}”. I guess it happens due to definition of cvx variable but don’t know how can I solve that.

BTW, I don’t know how I can upload my codes/data here.

Thanks again

Mark_L_Stone · May 9, 2019, 2:53am

I misread where the ptilda 's are. So SINR and sinr and linear-fractional.

I still have to tell you , you have so many different variants of your problem, with incomplete information on all of them, that I’m not sure what any of them are,

So I’m going to bout the burden back on you. Completely define a mathematical optimization problem. prove that it is a convex optimization problem (maximizing a concave function subject to convex constraints). if that can not be accomplished, then try to determine a CVX formulation is fruitless.

susan · May 9, 2019, 3:45pm

Thank you so much for your comment and sorry that I am struggling and failing in defining my problem clearly.

Could you please take a look at the above optimization problem one more time? I don’t think that SINR and sinr are the linear- fractional functions. In the above optimization problem the variable of interest is ptilda. As I have mentioned, the cvx should be used inside nested loops.

So the variable of interest for each cvx inside the nested loops over (k,m,l,i) is ptilda(k,m,l,i) which is a scalar. So, SINR is an affine function of ptilda(k,m,l,i) and sinr is a convex in the CVX variable ptilda(k,m,l,i) . I took the second derivative w.r.t. ptilda(k,m,l,i) and it is >= 0.

So the objective function is convex and by rewriting the constraint as log(convex) = - log(concave function), the constraint is convex and acceptable for cvx. right?

Now, when I run the code I got the error of “Cannot perform the operation: {real affine} ./ {real affine}” in the definition of SINR while it is affine in variable ptilda(k,m,l,i).

I guess the problem comes from defining the cvx variable. I don’t know how to tell cvx that the variable of interest is ptilda(k,m,l,i) while the rest of ptildas are given. in other words, we are going to optimize all of them at the same time. Does it make sense now?

Thanks again for your time

Mark_L_Stone · May 9, 2019, 3:59pm

SINR is linear fractional. I don’t know how you are going to deal with that inside log. So you need to prove that constraint is convex. otherwise, CVX can not be used for this problem.

sinr can be handled with inv_pos.

log(convex) is NOT allowed by CVX

help cvx/log

Disciplined convex programming information:
    log(X) is concave and nondecreasing in X. When used in CVX
    expressions, X must be concave.

Disciplined geometric programming information:
    log(X) is typically not used in geometric programs. Technically it
    possible to do so in certain advanced cases, because monomials and
    posynomials are treated by CVX as log-affine and log-convex
    constructs, respectively. However, such usage is undocumented and
    will not be officially supported.

susan · May 9, 2019, 4:19pm

Thank you so much for your quick reply.

Could you please tell me why SINR is linear fractional? the variable of interest, i., e, ptilda(k,m,l,i) that only shows up in the numerator while the other ptildas in the denominator have nothing to do with the ptilda (k,m,l,i).

My second question is I am using log(convex) = - log(concave function). Is it correct? since as you said, log(convex) is NOT allowed by CVX.

And the last question. how to define the cvx optimization variable? for specific ptilda(k,m,l,i) inside nested loop.

for k = 1 : K
for m = 1: M
for l = 1 : L
for i = 1 : I

            cvx_begin
            cvx_quiet(true);
            variable ptilda(k,m, l, i);
            
            objectvefunction = ...
            maximize(objectvefunction)
            cvx_end
        end
    end
end

end

Thank you very much. Appreciate your help

Mark_L_Stone · May 9, 2019, 4:41pm

I think you want for loops inslide cvx_begin … cvx_end, not outside.

I keep getting confused when you switch between problems.

log(convex) does not necessarily equal - log(concave function). You haven;t shown how the constraint with log having sinr in the argument is convex. i don;t see why it would be.

susan · May 9, 2019, 4:52pm

Thanks again for your quick reply.

Now I got confused too. I didn’t switch between problems( or at least I don’t think I am doing that). sorry for any inconvenience it may have caused.

regarding “log(convex) does not necessarily equal - log(concave function). You haven;t shown how the constraint with log having sinr in the argument is convex. i don;t see why it would be.”

I took the second derivative of the constraint with log having sinr in the argument w.r.t ptilda(k,m,l,i) and it is >= 0. That’s why I believe it is convex. Since log(convex) is not accepted by cvx I am using - log(1/convex). However, I am not sure if it is a right approach to take or not.

And thanks a million for mentioning that I need loops inside cvx. Let me see if it going to work.
Nope! it is not going to work put.
I got still error that SINR is {real affine} ./ {real affine}.

I think it is because cvx consider all ptildas as variable not only one specific one. Any idea how I can deal with this issue? Many thanks in advance

Mark_L_Stone · May 9, 2019, 5:02pm

convex expression <= constant and concave expression >= constant are convex constraints.
convex expression >= constant is not a convex constraint (unless the convex expression is affine, in which case it is also concave)

susan · May 9, 2019, 5:06pm

Is there any easy way that we can convert ( convex expression >= constant) to a convex constraint? Or I need to convexify the constraint as well?

susan · May 9, 2019, 5:23pm

Mark,
Could you please kindly tell me how I can apply cvx to the following optimization problem? assuming it is convex.

the variable of interest is p_{i} and we got K of these variables that we want to optimize.
Is cvx inside the for loop or outside of it?

Thanks again