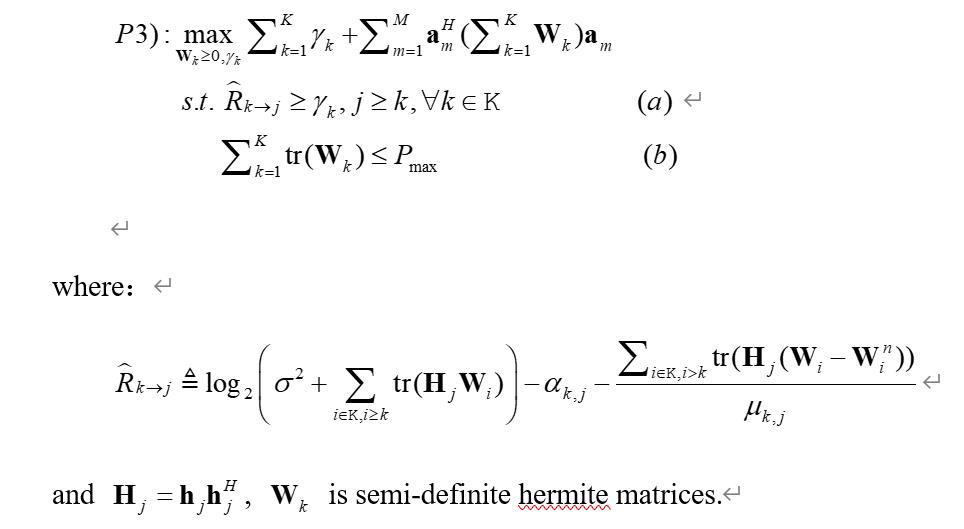How to build objective function and constraints using CVX

1

I’m new to CVX and thanks for your contribution to CVX and for helping users. I have successfully used CVX to solve the optimization problem I have built, but the procedure is too verbose and I don’t know how to modify it to a more simplified form under the CVX grammar rules.

As shown in the figure, I want to optimize multiple hermite matrices, and the current procedure is to set multiple optimization variables separately. If I want to set it as W(N,N,K), that is, K N-N matrix W, how should I construct the optimization objective function problem shown in the figure ?

微信图片_20220921203432
微信图片_20220921203432964×529 34.2 KB

In addition, the judgment is involved in the constraint (a), so I also use the method of brute force enumeration. Is it possible to rewrite them into a convenient form?

This is my program now:

function [rate_tmp,W_tmp,gamm,senor_power] = ISAC_sub1(h_matr,n_vec,a_matr,R_min,p_max,rho,alpha_vec,beta_vec,N,W_bfrc)
W_bfr1 = W_bfrc(:,:,1);
W_bfr2 = W_bfrc(:,:,2);
W_bfr3 = W_bfrc(:,:,3);
cvx_clear
cvx_begin sdp
variable W1(4,4) hermitian semidefinite
variable W2(4,4) hermitian semidefinite
variable W3(4,4) hermitian semidefinite
variable gamm(3)
maximize(sum(gamm)+real(a_matr(:,1)’*(W1+W2+W3)a_matr(:,1)+a_matr(:,2)’(W1+W2+W3)*a_matr(:,2)));
subject to
log(n_vec+real(trace(h_matr(:,1)*h_matr(:,1)’*W1))+real(trace(h_matr(:,1)*h_matr(:,1)’*W2))+real(trace(h_matr(:,1)*h_matr(:,1)’*W3)))/log(2)-alpha_vec(1)-(real(trace(h_matr(:,1)h_matr(:,1)’(W2-W_bfr2)))+real(trace(h_matr(:,1)h_matr(:,1)’(W3-W_bfr3))))/beta_vec(1)-gamm(1) >= 0

            log(n_vec+real(trace(h_matr(:,2)*h_matr(:,2)'*W1))+real(trace(h_matr(:,2)*h_matr(:,2)'*W2))+real(trace(h_matr(:,2)*h_matr(:,2)'*W3)))/log(2) -alpha_vec(2)-(real(trace(h_matr(:,2)*h_matr(:,2)'*(W2-W_bfr2)))+real(trace(h_matr(:,2)*h_matr(:,2)'*(W3-W_bfr3))))/beta_vec(2)-gamm(1) >= 0
                        
            log(n_vec+real(trace(h_matr(:,3)*h_matr(:,3)'*W1))+real(trace(h_matr(:,3)*h_matr(:,3)'*W2))+real(trace(h_matr(:,3)*h_matr(:,3)'*W3)))/log(2)-alpha_vec(3)-(real(trace(h_matr(:,3)*h_matr(:,3)'*(W2-W_bfr2)))+real(trace(h_matr(:,3)*h_matr(:,3)'*(W3-W_bfr3))))/beta_vec(3)-gamm(1) >= 0
                        
            log(n_vec+real(trace(h_matr(:,2)*h_matr(:,2)'*W2))+real(trace(h_matr(:,2)*h_matr(:,2)'*W3)))/log(2)-alpha_vec(4)-(real(trace(h_matr(:,2)*h_matr(:,2)'*(W3-W_bfr3))))/beta_vec(4)-gamm(2) >= 0
                        
            log(n_vec+real(trace(h_matr(:,3)*h_matr(:,3)'*W2))+real(trace(h_matr(:,3)*h_matr(:,3)'*W3)))/log(2)-alpha_vec(5)-(real(trace(h_matr(:,3)*h_matr(:,3)'*(W3-W_bfr3))))/beta_vec(5)-gamm(2) >= 0
                        
            log(n_vec+real(trace(h_matr(:,3)*h_matr(:,3)'*W3)))/log(2)-alpha_vec(6)-gamm(3) >= 0
            real(trace(W1)+trace(W2)+trace(W3)) <= p_max
    cvx_end
    W_tmp = zeros(N,N,3);
    W_tmp(:,:,1) = (h_matr(:,1)'*W1*h_matr(:,1))^(-1)*W1*h_matr(:,1)*h_matr(:,1)'*W1';W_tmp(:,:,2) = (h_matr(:,2)'*W2*h_matr(:,2))^(-1)*W1*h_matr(:,2)*h_matr(:,2)'*W2';W_tmp(:,:,3) = (h_matr(:,3)'*W3*h_matr(:,3))^(-1)*W3*h_matr(:,3)*h_matr(:,3)'*W3;
    rate_tmp = cvx_optval;
    gamm = sum(gamm);
    senor_power = abs(a_matr(:,1)'*(W1+W2+W3)*a_matr(:,1)+a_matr(:,2)'*(W1+W2+W3)*a_matr(:,2));

end

2

variable W(4,4,K) hermitian semidefinite

declares each of the K 2D slices, i.e., W(:,:,k),for k from 1 to K, to be hermitiam semidefimite

3

Yes and I got it. But I’m confused about how to express sum_k (W_k) and sum_m (a_m^HWa_m) in objective; as shown in figure.
Besides, it’s also a difficulty for me that how to write sum_{k<i<K} (trace(H_jW_i)) in constraint; does the function “sum” has such choice ability ? Sorry to bother you again

4

sum(W,3) sums over the 3rd dimension of W, i.e., all K of the 4 by 4 matrices, and results in a 4 by 4 matrix.

You can specify dimension to sum over as in “regular” MATLAB. But some of the options, such as ‘all’, do not work on CVX expressions (arguments).

help sum

 sum Sum of elements.
    S = sum(X) is the sum of the elements of the vector X. If X is a matrix,
    S is a row vector with the sum over each column. For N-D arrays, 
    sum(X) operates along the first non-singleton dimension.
 
    S = sum(X,'all') sums all elements of X.
 
    S = sum(X,DIM) sums along the dimension DIM.
 
    S = sum(X,VECDIM) operates on the dimensions specified in the vector 
    VECDIM. For example, sum(X,[1 2]) operates on the elements contained in
    the first and second dimensions of X.
 
    S = sum(...,TYPE) specifies the type in which the 
    sum is performed, and the type of S. Available options are:
 
    'double'    -  S has class double for any input X
    'native'    -  S has the same class as X
    'default'   -  If X is floating point, that is double or single,
                   S has the same class as X. If X is not floating point, 
                   S has class double.
 
    S = sum(...,NANFLAG) specifies how NaN (Not-A-Number) values are 
    treated. The default is 'includenan':
 
    'includenan' - the sum of a vector containing NaN values is also NaN.
    'omitnan'    - the sum of a vector containing NaN values
                   is the sum of all its non-NaN elements. If all 
                   elements are NaN, the result is 0.
 
    Examples:
        X = [0 1 2; 3 4 5]
        sum(X, 1)
        sum(X, 2)
 
        X = int8(1:20)
        sum(X)             % returns double(210), accumulates in double
        sum(X,'native')    % returns int8(127), because it accumulates in
                           % int8 but overflows and saturates.
5

I always thought that sum followed the special rules inside CVX. Thanks for detail answer and for my second problem, “sum_{k<i<K} (trace(H_jW_i))”, sum only a subset of terms in H_jW_i, can I first use a loop to compute the term containing the variable W and then add it to the inequality constraints?
such as:

subject to
for k = 1:K
tmp=0;
for j = k:K
tmp = tmp+H(;,j)'WH(:,j);
end
log(1+tmp)>=10;
end

6

Any CVX expressions which are summed still have to obey CVX’s DCP rules.

Yes, you can use for loops. I will let @jackfsuia tell you if there any any vectorizations possible which eliminate the need for for loops, or at least decrease the number of levels of for loop. The only advantages of for loops are possible shorter code, and faster executing code, which might be significant if k is “large” and k small. But there is nothing wrong with using for loops, if the CVX processing (not the solver time) is fast enough for you.

7

alright, thank you very much

8

P.S. it looks like your indexing might not be correct, but I’ll let you figure that out - it would be the same indexing required as if these were all MATLAB double precision variables.

9

Oh my last reply was a simple example, which is unrelated to the original question. So indexing might not be correct. A real constraint using loop constraint which I want to express:

subject to
for k = 1:K
for j =k:K
tmp1 = 0;tmp2=0;
for i = k:K
tmp1 = tmp1+real(trace(H(:,j)’*W(:,:,i)H(:,j)));
if i>K
tmp2 = tmp2+real(trace(H(:,j)’(W(:,:,i)-W_brf(:,:,i))*H(:,j)));
end
end
log(n_val+tmp1)-alpha(k,j)-tmp2/miu(k,j)-gamm(k)>=0;
end
end

where “log(n_val+tmp1)-alpha(k,j)-tmp2/miu(k,j)-gamm(k)>=0;” is the constraint I really want to achieve.(W and gamm are variables and other symbols are constant)

10

Are you all set now, or do you still have some difficulties? if you still have difficulties, please make a very clear statement of what they are.

11

Yes I will try it again. Thanks very much!