Hi
I solved a max minimum problem by using CVX, and I noticed that R_1=…=R_K=R^bar will hold when the optimal tau and R bar is obtained. I want to approve the result mathematically but I have no idea about it.
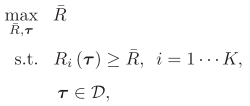
Thank you.
Hi
I solved a max minimum problem by using CVX, and I noticed that R_1=…=R_K=R^bar will hold when the optimal tau and R bar is obtained. I want to approve the result mathematically but I have no idea about it.
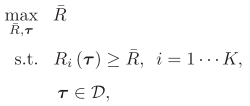
Thank you.
From what you have shown us, the optimal solution looks like it should be \bar{R} = min(R_i(\tau)) leaving aside whatever is going on with \tau, which your extract does not make clear.
Do you have a CVX question?
The result should be ![]() certainly. But CVX results of a max minimum problem furtherly show a interesting phenomenon that R_1=…=R_K=R^bar will also hold when the optimal tau and R bar is obtained.
certainly. But CVX results of a max minimum problem furtherly show a interesting phenomenon that R_1=…=R_K=R^bar will also hold when the optimal tau and R bar is obtained.
The problem is shown as
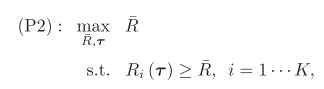
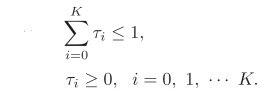
![]()
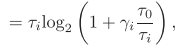
the code is shown as
K=5;
gammai = [57.3308 6.6528 0.6186 5.1297 5.5619]’;cvx_begin quiet
variable R_bar
variable tau_K
variable tau(K)
maximize R_bar
obj= -rel_entr(tau,tau+gammai*tau_K)/log(2) ;
obj>= R_bar
sum(tau)+tau_K<=1
tau >= 0
cvx_endR_bar
obj’
and the results is
R_bar = 0.3138
obj’ = 0.3138 0.3138 0.3138 0.3138 0.3138
That means the results not only satisfy ![]() ,but also meet R_1=…=R_K=R^bar furtherly. I’m not sure whether it is a common phenomenon for max minimum problem. And I want to seek help to approve it if that is a common phenomenon.
,but also meet R_1=…=R_K=R^bar furtherly. I’m not sure whether it is a common phenomenon for max minimum problem. And I want to seek help to approve it if that is a common phenomenon.
The proof problem has been done already. Many thanks for your help.
The optimal \tau_i are different for the different i such that R_i(\tau) come out equal, which apparently is the efficient, i.e., optimal, solution. I see nothing inherently suspicious about this. But then again, it is your model (or whatever paper or book it is from), so I defer to you as to how well it models whatever situation you are modeling.