How do I Structure this Optimization problem?

1

I have applied convex relaxation to a trajectory optimization problem and arrived at the coding stage in CVX. However, I have very little experience and am having trouble understanding the correct syntax. My optimization problem is defined as follows:
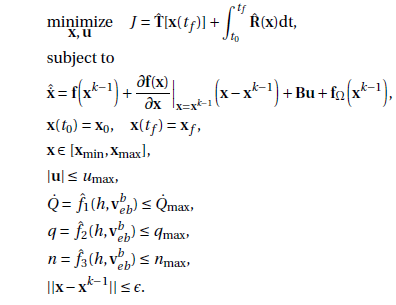
cvxquestion
where T(x(tf)) is some convexified terminal cost, R(x) is some convexified running cost, f(x^k-1) is the state derivative of a previous solution, x is the state, B is [zeros(14,1);ones(4,1)], u is delta1:4 dot, and f_omega is Earth rotational terms. The first two constraints are the initial and terminal, the next are state limits, then control magnitude limits, heating rate limit, dynamic pressure limit and normal force limit. The final is a trust region constraint.

For the moment I’m just interested in getting the first run of the optimization, and not in the successive nature, or in enforcing the trust-region. I’ve been trying (to no avail) for a week or so now to determine how to correctly explain to cvx what the state is, what the control is and how to iterate through the time-steps to solve the optimization problem.

Could anybody help?

1 Like
2

Decide on and declare your variables. You have a choice of using constraints to enforce relationships, or expression assignments which enforce a relationship “by definition”. Maybe x is an m by n matrix, in which the kth column is a vector for that time? So
variable x(m,n)

Then add the objective function and all the constraints. CVX doesn’t know anything about derivatives or integrals, so you will have to enter whatever they are into CVX, and do so in accordance with its DCP rules.

You should probably start with a very simplified model. Get that accepted by CVX. Then build up to the desired model.

2 Likes
3

Fantastic Mark thank you, could you direct me to a simple dynamic model which has been solved to optimality using CVX?

1 Like
4

Not that I know of, but you can look at CVX examples at http://cvxr.com/cvx/examples/ as well as on this forum.

2 Likes
5

Thanks Mark, you’ve been a great help.

1 Like