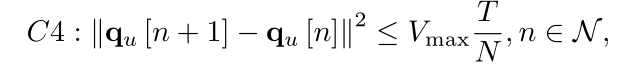
I did this as follows, but the error was reported.
cvx_begin
cvx_expert true
variable u_x(M,N)
variable u_y(M,N)
expression yj(M,N)
expression hjj(M,N)
expression hj(M,N)
expression rm(M,N)
expression rn(M,N)
expression rmsum(M,N)
expression gsum(M,N)
expression RMsum
for m = 1:M
for n=1:N
hj(m,n) = log(1+gamma0p(m,n))/(H^2+(x_fe(m,n)-use(m,1))^2+(y_fe(m,n)-use(m,1))^2)/log(2);
hjj(m,n)=(H^2+gamma0p(m,n)+(x_fe(m,n)-use(m,1))^2+(y_fe(m,n)-use(m,2))^2)(H^2+(x_fe(m,n)-use(m,1))^2+(y_fe(m,n)-use(m,2))^2);
yj(m,n)=hj(m,n)-gamma0p(m,n)(1/log(2))((u_x(m,n)-use(m,1))^2+(u_y(m,n)-use(m,2))^2-((x_fe(m,n)-use(m,1))^2+(y_fe(m,n)-use(m,2))^2))/ hjj(m,n);
rmsum(m,n)=w(m)BTt(m,n)yj(m,n)/(vN);
end
end
RMsum =sum(sum(rmsum));
maximize (RMsum);
subject to
square_pos(norms([[u_x,xf]-[x0,u_x];[u_y,yf]-[y0,u_y]],2,1))<=detaTVmax;
for m = 1:M
for n = 1:N
rm=rm+gammacf(m,n)^3+z(m,n);
rn=rn+(H^2+2((x_fe(m,n)-use(m,1))^2+(y_fe(m,n)-use(m,2))^2)-(u_x(m,n)-use(m,1))^2-(u_y(m,n)-use(m,2))^2)/((H^2+(x_fe(m,n)-use(m,1))^2+(y_fe(m,n)-use(m,2)))^2);
end
end
sum(rm(m,:)) <= etaP0bate0*sum(rn(m,:));
cvx_end
Some of the variables I defined at the beginning.
square_pos(norms([[u_x,xf]-[x0,u_x];[u_y,yf]-[y0,u_y]],2,1))<=detaT*Vmax;
Here’s the mistake
Error using CVX/CAT (line 40)
All dimensions but the one being concatenated (2) must be equal.
Error CVX/Horzcat (line 2)
y = cat( 2, varargin{:} );
Error Example2 (line 112)
square_pos(norms([[u_x,xf]-[x0,u_x];[u_y,yf]-[y0,u_y]],2,2))<=detaT*Vmax;