I have the following:
"
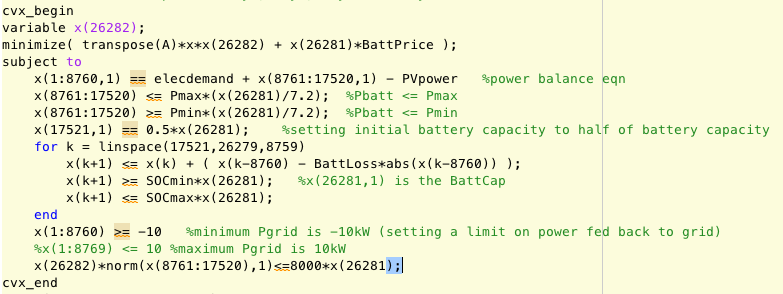
cvx_begin
variable x(26282);
minimize( transpose(A)*x*x(26282) + x(26281)*BattPrice );
subject to
x(1:8760,1) == elecdemand + x(8761:17520,1) - PVpower %power balance eqn
x(8761:17520) <= Pmax*(x(26281)/7.2); %Pbatt <= Pmax
x(8761:17520) >= Pmin*(x(26281)/7.2); %Pbatt <= Pmin
x(17521,1) == 0.5*x(26281); %setting initial battery capacity to half of battery capacity
for k = linspace(17521,26279,8759)
x(k+1) <= x(k) + ( x(k-8760) - BattLoss*abs(x(k-8760)) );
x(k+1) >= SOCmin*x(26281); %x(26281,1) is the BattCap
x(k+1) <= SOCmax*x(26281);
end
x(1:8760) >= -10 %minimum Pgrid is -10kW (setting a limit on power fed back to grid)
x(26282)*norm(x(8761:17520),1)<=8000*x(26281);
cvx_end
"
I believe the problem lies in 2 areas:
the objective: minimize(transpose(A)xx(26282) + x(26281)*BattPrice)
one of the constraints: x(26282)norm(x(8761:17520),1)<=8000x(26281)
I got the following error message:
"
Error using .* (line 262)
Disciplined convex programming error:
Invalid quadratic form(s): not a square.
Error in * (line 36)
z = feval( oper, x, y );
Error in convexproject_cycleconstraint (line 108)
minimize( transpose(A)xx(26282) + x(26281)*BattPrice );
"
How do I go about this error if I would like to keep that constraint on x(26282)?