In my optimal problem I have two constraints as following
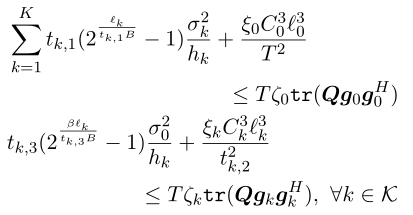
Q, t_k, l are all my variables. It’s a convex constraint but it can’t just solve for CVX.
(t3(1))sigma0/h(1)(power(2,beta*l(1)/B/(t3(1)))-1)+xi(1)*C(1)pow_pos(l(1),3)/(t2(1))^2 <= Talpha(1)real(trace(QH)). In this formula, l(1),t2(1),t3(1) and Q four variables. I want to know how to write this kind of constraint in cvx. Help needed. Thanks a lot.
Re-write 2^x as exp(log(2)*x)
Then use the exponential cone construct:
y*exp(y/x) <= z, with y > 0
can be written in CVX as
{ x, y, z } == exponential(1)
or alternatively,
x + rel_entr(y,z) <= 0
Declare z as a CVX variable, replace y*exp(y/x) by z, and add one of the above constraints.
Either way, CVXQUAD can be used without modification to your program, and is recommended for your problem CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions .
Thanks a lot, Mark~:grinning:
But I want to ask about the if the formula with variables l_k and t_k like
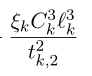 can be written in the CVX?
can be written in the CVX?
That doesn’t look convex to me. Why isn’t CVX accepting my model? READ THIS FIRST! You claim that constraint is convex, so show us the proof.
Hi, Mark~
Can we made this formula as a perspective function as following
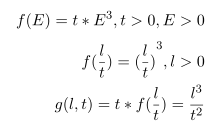
You didn’t tell us before that l > 0. The determinant of the Hessian = 0, therefore at least one of the two eigenvalues is always zero. Examination of the trace of the Hessian shows that the function is convex for l >= 0 and certain combinations of t and l < 0; and is concave everywhere else.The Hessian is never indefinite.
Given that the function is not convex over its entire natural domain, and is convex only for certain combinations of t and l < 0, I am not optimistic you can get it into CVX for the entirety of its convex region. Perhaps you or another forum reader can determine whether there is a formulation which can be entered into CVX with the constraint that l >= 0 .
Surely something like (n+1)-power-over-n-power should be representable by iterating quad-over-lins. It corresponds to a power cone. Homogenizing an example from https://docs.mosek.com/modeling-cookbook/cqo.html#simple-sets-involving-power-functions we have that xy^2\geq z^3 with x,y,z\geq 0 is equivalent to sy\geq z^2,\ xz\geq s^2.
I’m so sorry that I just saw the answer. Thanks a lot.
 Thanks very much for your answer and also apologize for that I miss the answer before…
Thanks very much for your answer and also apologize for that I miss the answer before…
Thanks Dixiao.
It is true that x^3/t^2<=z can be equivalently turned into yt>=x^2, zx>=y^2 according to the topic you linked, and we can represent x^3/t^2 with z by introducing another two variables z and y and adding the two constraints. However, the two constraints yt>=x^2, zx>=y^2 are not convex and can not be used in CVX. By doing that, I have the following error:
%%%%%%%%%%%%%%%%%%%%%%%
Error using .* (line 262)
Disciplined convex programming error:
Invalid quadratic form(s): not a square.
Error in * (line 36)
z = feval( oper, x, y );
Error in Sample_Trajectory_CVX (line 45)
x2^2-y2*t2<=0;
%%%%%%%%%%%%%%%%%%%%%%
Do you know how to solve this error?
You have to use lorentz_cone, or whatever it is called in cvx, rather than write the non-convex version of these constraints.
Thanks so much. I think the CVX function ‘rotated_lorentz(n)’ works for this case.
Hi, Dixiao, this problem also troubles me for a long time. Could you show the correct code for l^3/t^2, thank you very much!
As shown above by @Michal_Adamaszek
xy^2\geq z^3 with x,y,z\geq 0 is equivalent to sy\geq z^2,\ xz\geq s^2.
The latter can be written in CVX as
variables x y z s
{z,s,y} == rotated_lorentz(1)
{s,x,z} == rotated_lorentz(1)
Then use x in place of z^3/y^2
Hi @Mark_L_Stone,
I am dealing with a similar constraint in my optimization which is as follows:
variables x, z
variable y(1,2)
x+((norm(y))^2/x)+z+((norm(y))^3/x^2) <= constant
The first term I was managed to represent using quad_over-lin(). Could you please help me to represent the last term in an acceptable form by CVX?
Many Thanks in advance!
Nithin
Hi, do you now solve your problem? I have similar problem to you and still stuck in this.
I flubbed that one because I wasn’t accounting for norm being the thing that was cubed in @Nithin_Babu’s post.