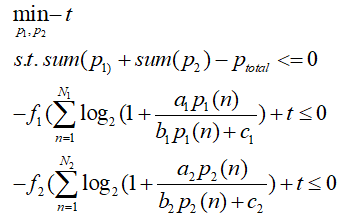Thanks so much for your professional answer!!! The cvx constraint condition question is solved by using the method that
[quote=“Mark_L_Stone, post:2, topic:9149, full:true”]
I think you can apply the reformulation in Can CVX solve this kind of function {x-log(1+0.01*x/(x+1))} to each summation term in the constraints.
In the future, please copy and paste code into your post, using Preformatted text icon, rather than posting an image of your code.
[/quote]. Thank you very very much!!! I will not use the picture to represent my question any more. I’m so so sorry about that.
In my simulation, I meet another question which troubled me.
I use the cvx 2.2 and mosek 9.1.9 to solve the question
cvx_begin
variable t
variable p1(N1,1)
variable p2(N2,1)
minimize(-t)
subject to
(-1)*t<=0;
for n1=1:N1
(-1)*p1(n1,1)<=0;
end
for n2=1:N2
(-1)*p2(n2,1)<=0;
end
sum(p1)+sum(p2)-p_total<=0;
for i1=1:NO1
value1=0;
for ii1=1:N1
value1=value1+log(1+B1_Cell{i1,5}(ii1,1)-B1_Cell{i1,5}(ii1,1)*B1_Cell{i1,6}(ii1,1)*inv_pos(p1(ii1,1)+B1_Cell{i1,6}(ii1,1)))/log(2);
end
(-1)*value1+t<=0;
end
for i2=1:NO2
value2=0;
for ii2=1:N2
value2=value2+log(1+B2_Cell{i2,5}(ii2,1)-B2_Cell{i2,5}(ii2,1)*B2_Cell{i2,6}(ii2,1)*inv_pos(p2(ii2,1)+B2_Cell{i2,6}(ii2,1)))/log(2);
end
(-1)*value2+t<=0;
end
cvx_end
At first few times, the matlab output is normal, however, after few times, the output of matlab becomes :
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 1039
Cones : 1048
Scalar variables : 3169
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 20
Optimizer - solved problem : the primal
Optimizer - Constraints : 1039
Optimizer - Cones : 1048
Optimizer - Scalar variables : 3169 conic : 3144
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 7605 after factor : 1.59e+04
Factor - dense dim. : 0 flops : 4.89e+05
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.5e+01 1.5e+15 1.2e+04 0.00e+00 1.150469465e+04 0.000000000e+00 1.0e+00 0.06
1 7.0e+00 7.3e+14 8.0e+03 -1.00e+00 1.151098091e+04 7.354833266e+00 4.8e-01 0.17
2 1.1e+00 1.1e+14 3.1e+03 -1.00e+00 1.149712701e+04 4.931274102e+00 7.4e-02 0.19
3 2.6e-01 2.7e+13 1.5e+03 -1.00e+00 1.145411878e+04 4.627260324e+00 1.8e-02 0.20
4 1.7e-01 1.8e+13 1.3e+03 -1.00e+00 1.142662690e+04 4.376172671e+00 1.2e-02 0.22
5 4.6e-02 4.8e+12 6.5e+02 -1.00e+00 1.119203505e+04 2.910704591e+00 3.2e-03 0.22
6 1.2e-02 1.2e+12 3.3e+02 -1.00e+00 1.028178796e+04 1.935104668e+00 8.2e-04 0.23
7 2.9e-03 3.0e+11 1.6e+02 -1.00e+00 6.488447257e+03 1.570595044e+00 2.0e-04 0.25
8 7.3e-04 7.6e+10 8.1e+01 -1.00e+00 -8.479353955e+03 1.120403332e+00 5.0e-05 0.27
9 1.6e-04 1.7e+10 3.8e+01 -1.00e+00 -7.992730275e+04 8.586086394e-01 1.1e-05 0.28
10 2.0e-05 2.1e+09 1.3e+01 -1.00e+00 -7.212370065e+05 7.795012563e-01 1.4e-06 0.28
11 2.5e-06 2.6e+08 4.8e+00 -1.00e+00 -5.851586243e+06 6.985123830e-01 1.7e-07 0.30
12 2.9e-07 3.0e+07 1.6e+00 -1.00e+00 -5.011191746e+07 5.715748955e-01 2.0e-08 0.31
13 3.0e-08 3.1e+06 5.2e-01 -1.00e+00 -4.899735512e+08 -2.764072256e-03 2.0e-09 0.31
14 3.9e-10 4.1e+04 5.8e-02 -1.00e+00 -3.713480280e+10 -6.837846132e-03 2.7e-11 0.33
Optimizer terminated. Time: 0.39
Interior-point solution summary
Problem status : DUAL_INFEASIBLE
Solution status : DUAL_INFEASIBLE_CER
Primal. obj: -9.9998258127e-01 nrm: 7e+01 Viol. con: 3e-09 var: 3e-11 cones: 0e+00
Optimizer summary
Optimizer - time: 0.39
Interior-point - iterations : 14 time: 0.33
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Infeasible
Optimal value (cvx_optval): +Inf
the picture means that:
A nonexistent field ‘sol’ was referenced
error in cvx_mosek
error in cvxprob/solve
error in cvx_end
error in optimization method
Is my matrix’s column number to large? or because the optimization function became to large? I try to decrease matrix’s column and the value1’number ,but the problem still exits. Would you tell me how to deal the problem if you know somthing ahout it? I really appreciate your help!!!