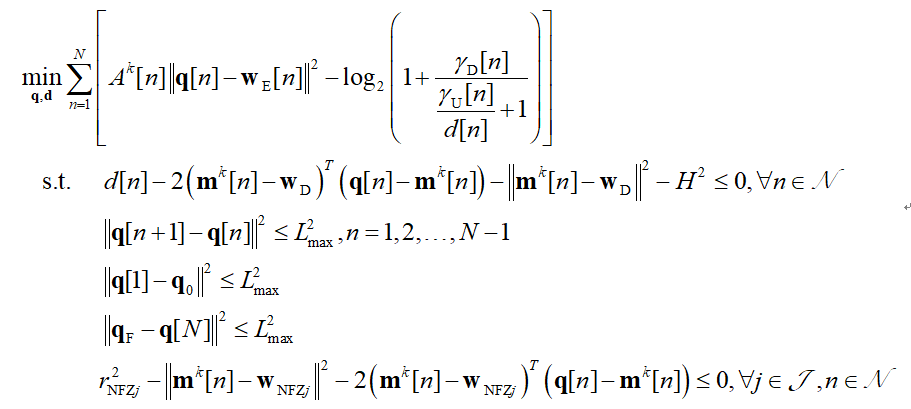How can I formulate this in CVX

Nonconvex
1

image
image911×409 11.9 KB

cvx_begin
variables q_ite(2 * N, 1) d(N, 1)
expression R(N, 1)
for i = 1 : N
R(i, 1) = A(i, 1) * square_pos(norm(q_ite(2 * i - 1 : 2 * i, 1) - w_E(2 * i - 1 : 2 * i, 1))) - (log(1 + gamma_D(i, 1) - (gamma_U(i, 1) * gamma_D(i, 1) * inv_pos(gamma_U(i, 1) + d(i, 1)))) / log(2));
end
minimize (sum®);
subject to
for i = 1 : N
d(i, 1) - d_UD(i, 1) - 2 * (q(2 * i - 1 : 2 * i, 1) - w_D)’ * (q_ite(2 * i - 1 : 2 * i, 1) - q(2 * i - 1 : 2 * i, 1)) <= 0;
for j = 1 : J
(r_NFZ(1, j))^2 - (norm(q(2 * i - 1 : 2 * i, 1) - w_NFZ(:, j)))^2 - 2 * (q(2 * i - 1 : 2 * i, 1) - w_NFZ(:, j))’ * (q_ite(2 * i - 1 : 2 * i, 1) - q(2 * i - 1 : 2 * i, 1)) <= 0;
end
if i == N
square_pos(norm(q_F - q_ite(2 * i - 1 : 2 * i, 1))) <= (L_max)^2;
else
square_pos(norm(q_ite(2 * (i + 1) - 1 : 2 * (i + 1), 1) - q_ite(2 * i - 1 : 2 * i, 1))) <= (L_max)^2;
end
end
square_pos(norm(q_ite(1 : 2, 1) - q_0)) <= (L_max)^2;
cvx_end

2

Hello, Thanks for posting.

It looks like there is nothing preventing d[n] from being negative, in which case summands in the objective function can be concave.

3

Thank you very much! I have added a constrain d[n] >= H^2 that ensure d[n] is positive, but it also has some errors.

01
01883×438 13.6 KB

cvx_begin
variables q_ite(2 * N, 1) d(N, 1)
expression R(N, 1)
for i = 1 : N
R(i, 1) = A(i, 1) * square_pos(norm(q_ite(2 * i - 1 : 2 * i, 1) - w_E(2 * i - 1 : 2 * i, 1))) - (log(1 + gamma_D(i, 1) - (gamma_U(i, 1) * gamma_D(i, 1) * inv_pos(gamma_U(i, 1) + d(i, 1)))) / log(2));
end
minimize (sum®);
subject to
for i = 1 : N
d(i, 1) - d_UD(i, 1) - 2 * (q(2 * i - 1 : 2 * i, 1) - w_D)’ * (q_ite(2 * i - 1 : 2 * i, 1) - q(2 * i - 1 : 2 * i, 1)) <= 0;
- d(i, 1) + H^2 <= 0;
for j = 1 : J
(r_NFZ(1, j))^2 - (norm(q(2 * i - 1 : 2 * i, 1) - w_NFZ(:, j)))^2 - 2 * (q(2 * i - 1 : 2 * i, 1) - w_NFZ(:, j))’ * (q_ite(2 * i - 1 : 2 * i, 1) - q(2 * i - 1 : 2 * i, 1)) <= 0;
end
if i == N
square_pos(norm(q_F - q_ite(2 * i - 1 : 2 * i, 1))) <= (L_max)^2;
else
square_pos(norm(q_ite(2 * (i + 1) - 1 : 2 * (i + 1), 1) - q_ite(2 * i - 1 : 2 * i, 1))) <= (L_max)^2;
end
end
square_pos(norm(q_ite(1 : 2, 1) - q_0)) <= (L_max)^2;
cvx_end

4

Even if that constraint makes the optimization problem convex, the -log2 term is not convex over the entirety of its natural domain, which historically is not a favorable indicator for the prospects of a DCP-compliant reformulation. I will not rule out that some wizard will come along who can provide such a reformulation, but I think it unlikely.

5

Thank you for your reply!