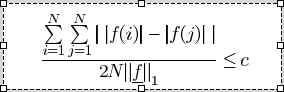Help: cvx codes about convex

Nonconvex
1 
cvx_begin
    variable W(1,dimC(3))
    minimize(W*normPerSliceDiag*W');
    %TotalWNorm = norm(W*normPerSliceDiag,1);
    subject to
        norm(W,1)<=1;
        for RepeatT =1:dimC(3),
        for RepeatK =1:dimC(3),
  (1)          sum(sum(abs(abs(W(RepeatT)*normPerSlices(RepeatT))-abs(W(RepeatK)*normPerSlices(RepeatK))))) >= 2*GiniMax*dimC(3);
        %1+2*sum(abs(W(RepeatT)*normPerSlices(RepeatT))*(dimC(3)-RepeatT+0.5))/(dimC(3)*TotalWNorm)>GiniMax;%%
(2)      % 1 + 2*sum(abs(W(RepeatT)*normPerSlices(RepeatT))*(dimC(3)-RepeatT+0.5)) > 2*GiniMax*(dimC(3)*norm(normPerSliceDiag,1));%%
        %(1-2*sum(abs(AB{i})*(dimC(3)-i+0.5)/dimC(3)))>GiniMax;
        end
    end
cvx_end

the above code says:
(1):Disciplined convex programming error:
Illegal operation: {convex} - {convex}
or
(2):Disciplined convex programming error:
Illegal operation: {convex} - {real constant}

I am perplexed and I don’t know how to do. Please help, thanks!

2

Your problem must be convex. Do you have proof that your model is convex? If not you are likely to use the wrong tool.

This

{convex} - {convex}

most likely means you have something like

f(x)-g(x) <= 0

where both functions are convex, but that does NOT in general specify a convex set. An example is

x^2-y^2 <= 0

3

As @Erling says
sum(sum(abs(abs(W(RepeatT)*normPerSlices(RepeatT)) - abs(W(RepeatK)*normPerSlices(RepeatK))))) >= 2*GiniMax*dimC(3);
does not follow CVX’s DCP rules, and doesn’t look to me that it can be reformulated as a convex constraint.

4

Thank you very much! I will check my convex model!

5

Thank you very much! The model is convex, but I can try it by what you refer to YALMIP

6

Thank you very much! My model is convex, but it may not satisfy the DCP rulesets!

7

Please prove your model is convex.

You can try YALMIP, which will at least accept your problem, although it may not necessarily be easy to solve.

8

Do you have nice formulation using usual math you can show us? E.g. from a paper.

9

Yes, your suggestion is very efficient! Many thanks!

10

%E6%8D%95%E8%8E%B7
This is Gini Index formula

11

That does not look convex to me.

12

The Gini Index formula you show here is convex if you assume f_i \geq 0 in which case you can change the formula to \sum_i \sum_j | f_i - f_j | \leq 2cN S and S = \sum_j f_j. Maybe this fact can help you reformulate your mathematical model?