I have defined "bi,di_bar,t1,t & zi’ as variables in MATLAB code. But in constraint among all variable “t & zi” is not giving values as defined in constraint equation. “t and zi” is taking automatically 0 and 1 respectively. What to do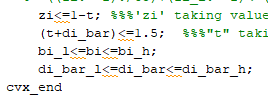 !
!
Please show a minimal complete reproducible example, including all input data, the solver and CVX output, and the evidence of whatever you think is not correct about the results.
Please copy and paste code using Prefomatted text icon, rather than posting an image of code.
Thank you for reply. I am posting code. I want to optimize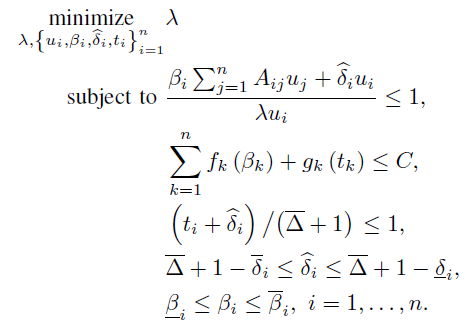
`
clc
clear
close all
uj=[2;4;6];
ui=[3;6;9];
N=length(uj);
ti_l=0.1;ti_h=0.5;
bi_l=0.0042ones(3,1);bi_h=0.021ones(3,1);
di_bar_h=1.4ones(3,1);di_bar_l=1ones(3,1);
A=[1,2,3;2,4,5;3,5,6];
A_new=Auj;
tri=1.5ones(3,1);
cvx_begin gp quiet
variables lem bi(N) di_bar(N) t1(N) t(N) t3(N) zi
zi_h=0.9;
zi_l=0.5;
minimize lem
subject to
for i=1:3
d(i)=di_bar(i)*ui(i);
((bi(i).*A_new(i))+d(i))/(lem*ui(i))<=1;
end
x=((bi_h.^-1)./((bi_l.^-1)-(bi_h.^-1)));
y=(zi_l^-1/((zi_h^-1)-(zi_l^-1)))
sum(t1-x)<=100;
((bi.^-1)./t1)+(bi_h.^-1)<=(bi_l.^-1);
zi<=1-t;
(t+di_bar)<=1.5;
bi_l<=bi<=bi_h;
di_bar_l<=di_bar<=di_bar_h;
cvx_end
fprintf('t %2.5f \n',t)
fprintf('bi %2.5f \n',bi)
fprintf('di_bar %2.5f \n',di_bar)
fprintf('zi %2.5f \n',zi)
`
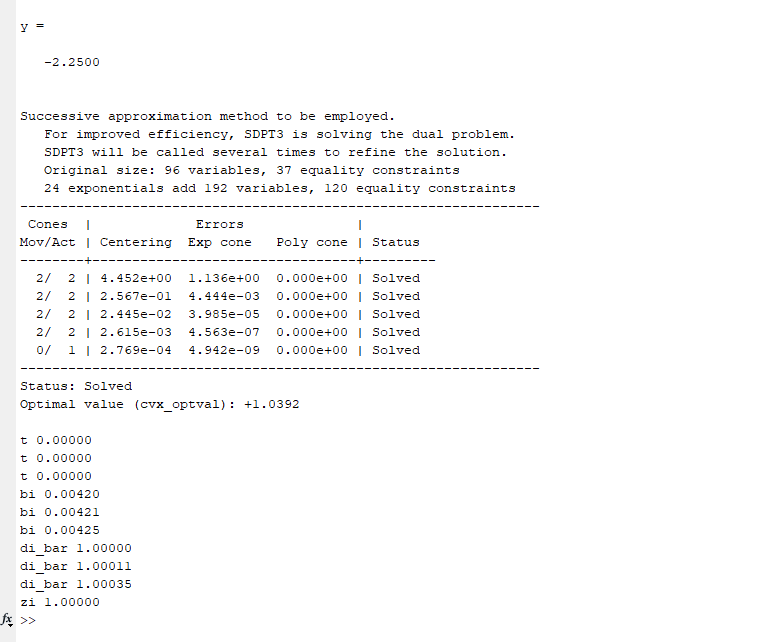
Do not use `quiet’ Re-run this, and show us all the solver and CVX output (and please read it yourself);; and show us what you believe is incorrect about the solution.
Are you claiming some constraints are violated? Or you just don’t “like” the solution (t = 0, zi = 1)? if you don’t like the solution, perhaps your model needs improvement, or it’s a consequence of this input data.
I have expressed t+di_bar<=1.5 and there are 3 difference values of “di_bar” so I am expecting to have 3 different values of “t”. But here all 3 values of “t” are “0” i.e. same for “zi”. this is my doubt why “t and zi” variable are taking only one value
Changing
(t+di_bar)<=1.5;
to
(t+di_bar)<=1
results in the same optimal objective value.
And, whether 1.5 or 1 on the RHS of that constraint, optimal t is a vector of zeros and optimal di_bar is a vector of ones, ignoring solver tolerance deviations from exactly these numbers.
If that constraint is eliminated, the optimal objective value is unchanged, but optimal t is now a vector of ones, as is optimal di_bar.
If you don’t like this, then your model and/or input data need adjustment.
Yeah, if I remove that constraint then from where vector t is getting its elements/values 1. If no operation has done in t then its must be empty set
If t doesn’t do anything, its optimal value can be anything (nonnegative due to being in gp mode). This is different from YALMIP, in which irrelevant variables which can be removed from the model have value NaN after optimization completes…
In gp mode, all variables are automatically constrained to be nonnegative. So
zi<=1-t;
(t+di_bar)<=1.5;
is only constraining di_bar to be <= 1.5, because the first of those constraints allows t = 0, with no adverse impact elsewhere. But di_bar is already constrained to 1 <= di_bar <= 1.4.
Anyhow, between your model and your code, rethinking and rework is probably needed. I have no idea what your model is supposed to do, so I leave that to you.