Disciplined convex programming error: Invalid operation: {positive convex} ./ {real affine}

1

hello to all.

I’m trying to soleve {

1

}
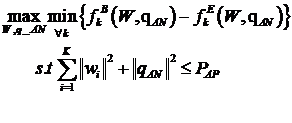
with
2

3
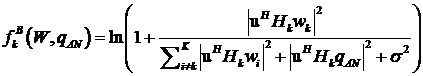
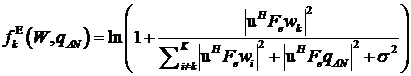
We could find a lower bounding concave function for the first,and upper bounding convex for the second.
4
5
6
7
8

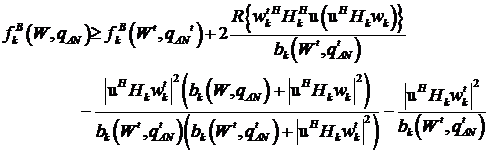
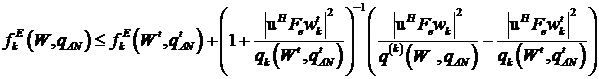
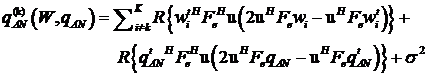
and this is my code
function [w_new,q_AN_new] = cvx_solver_w_Q_AN(P_AP,w,q_AN,u,f_B,f_E,b,q,H,Num_user,F_e,sigma_U,sigma_E)
M = size(w,1);
N = size(w,2);
result = 0;
cvx_begin
% ，x w,q_AN
variable x
variable w_new(M,N)
variable q_AN_new(M,1)

for k =1:1:Num_user
    result = result + norm(w_new(:,k))^2;
end
result + norm(q_AN_new)^2 <= P_AP;

%%
%
for k =1:1:Num_user
sum_1 = 0; %
sum_2 = 0;
%
for i =1:1:Num_user
if i == k
continue;
else
sum_1 = sum_1 + norm(u’*H(:,:,k)*w_new(:,i))^2;
sum_2 = sum_2 + real(w(:,i)‘F_e’u(2u’F_ew_new(:,i)-u’F_ew(:,i)));
end
end
b_new(k,:slight_smile: = sum_1 + norm(u’*H(:,:,k)q_AN_new)^2 + sigma_U;
q_new(k,:slight_smile: = sum_2 + real(q_AN’F_e’u(2u’F_eq_AN_new-u’F_eq_AN))+sigma_E;
%
end
for k =1:1:Num_user
f_new_B(k,:slight_smile: = f_B(k,:slight_smile: + 2real(w(:,k)’*H(:,:,k)‘uu’*H(:,:,k)*w_new(:,k))/b(k,:)-…
(norm(u’*H(:,:,k)w(:,k))^2(b_new(k,:)+norm(u’*H(:,:,k)w_new(:,k))^2))/(b(k,:slight_smile:(b(k,:)+norm(u’*H(:,:,k)*w(:,k))^2))-norm(u’*H(:,:,k)*w(:,k))^2/b(k,:);

    f_new_E(k,:) = f_E(k,:) + inv_pos((1+norm(u'*F_e*w(:,k))^2/(q(k,:)))*(norm(u'*F_e*w_new(:,k))^2./(q_new(k,:)) - norm(u'*F_e*w(:,k))^2/(q(k,:))));      
end

maximize x  % target

subject to
for k = 1:1:Num_user
    x <= f_new_B(k,:) - f_new_E(k,:);
end

cvx_end
result_old = cvx_optval;
end
the error is
Disciplined convex programming error:
Invalid operation: {positive convex} ./ {real affine}
cvx_solver_w_Q_AN (line 37)
f_new_E(k,:slight_smile: = f_E(k,:slight_smile: +
inv_pos((1+norm(u’F_ew(:,k))^2/(q(k,:)))*(norm(u’F_ew_new(:,k))^2./(q_new(k,:))
- norm(u’F_ew(:,k))^2/(q(k,:))));

2

Welcome to the forum!

For your objective
max min {expression}
have you proven that expression is concave, which is required for the optimization problem to be convex?

I will assume it is not unless you show otherwise.

3

Hi Mark,thanks for answering my question.Yes ,the original expression is not concave,so we find the concave approximation of the expression.By the following approximation.

4 the first part of the expression

and the second part of the expression is
6

so we can get a lower bound approximation of (fk_B-fk_E).I found two articles that used this method to get an approximate concave function.

4

I don’t have the energy to decipher all the notation and figure out what those expressions amount to.

How did those articles prove the requisite concavity and convexity of the two “terms”? Can you formulate them consistent with CVX’s rules? Did the papers implement this in CVX or other convex optimization tool?

5

Yep,these papers used the CVX tool to solve the problem .This is where I get confused and I can’t reproduce their results.I’m going to analyze this model in detail.Thanks for your help .

7

I recommend you to prove its Concavity and convexity in effective way ，such as Judge whether his hessian matrix is positive semidefinite or not ，then ,you should read The DCP ruleset¶, beacause though your function are convex but It is possible that CVX will still refuse you

8

Perhaps send an email to the authors requesting more details on how CVX was used.

9

Thanks for your answer.I thought My second convex approximation doesn’t conform to the DCP rule in CVX, but It’s not clear to me how to express this convex approximation in CVX either.But thank you again for your answer

10

yes,I have emailed the authors asking for more details.Thank you Mark,Thank you for your contribution to the forum.