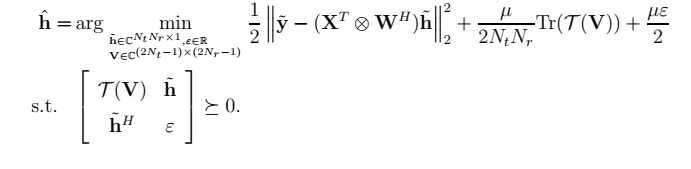Disciplined convex programming error: Illegal operation: {convex} + {complex affine}

Nonconvex
1

hello to all.

I’m trying to solve {

ffff
ffff.jpg691×169 16.4 KB
}
optimization problem using CVX. here epsilon is a real value. mu is a predefined real value. h is a vector to be estimated and is a complex vector. T(V) is a block toaplitz matrix. this problem is from an article and the matrix V in the block toaplitz matrix is a complex matrix. I use the following code on CVX but I get an error:
“Disciplined convex programming error:
Illegal operation: {convex} + {complex affine}”
here is my code. can anybody help me?

NrNt = Num_BS_Antennas*Num_MS_Antennas;
mu = sqrt(No)sqrt(NrNtlog10(NrNt));

cvx_begin sdp

variable hPrime(NrNt) complex
variable ep
variable V(2Num_BS_Antennas-1,2Num_MS_Antennas-1) complex
T = toeplitz_main(V);
% variable T(NrNt,NrNt) hermitian toeplitz
minimize (.5sum_square_abs(y-Dic_AtomhPrime)+(mu/2*NrNt)trace(T)+muep/2 );

subject to
[T hPrime;
hPrime’ ep]>=0;

cvx_end

2

function [blk_T] = toeplitz_main(V)
% V = [1 2 3; 4 5 6; 7 8 9];
blk_T = block_toeplitz(V);
% disp(blk_T);
end

function [t] = toeplit(v)
le = length(v);
center = ceil(le/2);
v1 = v(1:center);
v2 = v(center:end);
t = toeplitz(v1,v2);
end

function [block_T] = block_toeplitz(V)
[V_rows, V_cols] = size(V);
N_r = ceil(V_cols/2);
center_col_index = N_r;
N_t = ceil(V_rows/2);

block_T = [];
for i = 0 : (N_r - 1)
    block_T_col = [];
    for j = (center_col_index - i) : (center_col_index + N_r - 1 - i)
        block_T_col = [block_T_col ; toeplit(V(:, j))];
    end
    block_T = [block_T block_T_col];
end

end

3

Where is the error message occurring?

Does T = toeplitz_main(V); execute without error message? If so, what is the result of whos T ?

What is the result of whos just prior to where the error message is occurring?

4

error occurs here
(minimize (.5sum_square_abs(y-Dic_AtomhPrime)+(mu/2*NrNt)trace(T)+muep/2 ):wink:

5

Along the lines of my previous answer, look at the individual terms in the objective and see what they are.

Is trace(T) complex? If so, how can you have a complex additive term as part of an objective function which mist evaluate to a real scalar? Perhaps it is supposed to be real(trace(V)) ?

1 Like