Here I have an error of the constraint:
Disciplined convex programming error:Invalid constraint: {concave} == {constant}
The constraint is as follows:
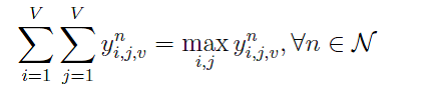
I can prove it is quasi linear by the defination, and from Boyd’s textbook, the domain and sublevel set of quasi linear is convex, thus the constraint should be convex constraint.
Why cvx give the error ? Is the CVX could not solve this problem or I have some misunderstanding about quasi linear?
WISH somebody can give me an answer, thanks a lot!
Nonlinear equality constraints are not allowed. See Why isn't CVX accepting my model? READ THIS FIRST! .
Perhaps you need to re-read Boyd’s book.
What exactly are you trying to accomplish here? That constraint seems to effectively force y_{i,j,v}^n = 0 for all i,j. But yes, Mark is right; if you had read the documentation and the FAQ you’d know why CVX cannot accept this constraint.
Thanks a lot. I should read the tips first before asking.
Thanks for your answer!
Thanks for your answer, Michael
The constraint forces only the maximum value of y can be nonzero, the others are all zero. I am not sure if there are other alternative formulations for this meaning. What do you think about this formulations? Is it Ok or there exist easier formulation?
By the way, I am still not sure whether the quasilinear constraint are convex constraint or not, and if it is and cannot transform to a DCP rules, is there any solvers for solving the problem? Or I just design althgrithem by myself?
Thanks for your reading !
I think you can do what you want using a Big M approach with the MIDCP capability of CVX. To do so, you will need finite upper bounds om the variables, and need to set a small positive value as the dividing line between elements equal to zero vs. greater than zero.
I am assuming (modeling) there being exactly one maximum element of y (i.e., no ties for maximum are possible). If you don’t want this, some modification to my solution will be needed.
To make things simple, I’ll assume y is an n by 1 array, whose upper bounds are provided by the n by 1 input vector upper_bound , and min_pos_value will be the minimum value considered to be non-zero. I introduce an n by 1 binary variable non_zero, which is 0 or 1 respectively for corresponding y element is zero or >= min_pos_value. The extension to matrix variables is straightforward.
Make upper_bound as small as you can. You may need some care in setting min_pos_value. I can not test this program, so no guarantees.
min_pos_value = 1e-5;
cvx_begin
variable y(n)
variable non_zero(n) binary
% Insert objective function and the rest of the constraints
min_pos_value*non_zero <= y <= upper_bound.*non_zero
sum(non_zero) == 1
cvx_end
As can be seen, if non_zero(i) == 0, then 0 <= y(i) <= 0, i.e, y(i) == 0. If non_zero(i) == 1, then min_pos_value <= y(i) <= upper_bound(i). Exactly one element of non_zero must equal 1.
Thanks, thanks a lot for your analysis !
I understand what you want to do – indroduce a binary variable to represent the constraint, I believe your algorithm is working. However, when the binary variable is introduced, would the time complexity be very high?
So I am not sure whether it can be solved in polynomial time.
Anyway, thanks for your answer. It really gives me an alternative way.
Per https://en.wikipedia.org/wiki/Integer_programming
Integer programming is NP-complete. In particular, the special case of 0-1 integer linear programming, in which unknowns are binary, and only the restrictions must be satisfied, is one of Karp’s 21 NP-complete problems.
Nevertheless, large MILPs are routinely solved nowadays. You haven’t told us what the number of elements in y is, nor what the rest of the problem is. MISOCPs, which can be solved by Gurobi or MOSEK under CVX can be more difficult. But as the saying goes, the proof is in the pudding, so give it a try. If you can formulate problems of different sizes, perhaps start with smaller size and work your way up. It’s always a bit of a crapshoot with mixed integer problems of significant size.
The tighter (smaller) you can make upper_bound, the easier your problem should be to solve.
If you can prove P = NP, you’ll be famous.
haha, I got what you mean.
I will have a try, maybe someday I’ll be famous because the proof of P=NP.
Thanks for your answer.