clc;
J=6;
K=4;
H = (randn(K,J)+sqrt(-1)*randn(K,J))/sqrt(2);
N0=10.^(-17.4).*10.^4;
F1=[1 1 1 0 0 0;1 0 0 1 1 0;0 1 0 1 0 1;0 0 1 0 1 1];
for R=20
path_loss=128.1+37.6.*log10(R.*10^-3);
loss=(10.^(0.8)).*(10.^(path_loss/10));
h=sort(abs(H).^2,2,'descend')./(loss);
cvx_begin
variable pkj(4,6)
expression r(4,6)
expression p(4,6)
p=F1.* pkj;
for k=1:4
r(k,2)=log(1+p(k,2).*h(k,2)./(N0+p(k,1).*h(k,1)));
end
u=sum(r(:,2));
maximize u
subject to
sum(p)<=0.05;
p>=0;
cvx_end
endp(k,2).*h(k,2)./(N0+p(k,1).*h(k,1)) violates CVX’s DCP rules.
Have you proven (each matrix element of log(1+p(k,2).*h(k,2)./(N0+p(k,1).*h(k,1))) is concave? It certainly is not with generic parameter values
the above code optimizing model is 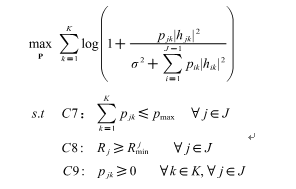 it can be solved by lagrangian multiplier method. so I want to ask this problem can be solved by CVX?
it can be solved by lagrangian multiplier method. so I want to ask this problem can be solved by CVX?
O.k., I think the objective function is concave. I think @Michal_Adamaszek’s solution at Can CVX solve this kind of function {x-log(1+0.01*x/(x+1))} can be adapted for this problem. I’ll let you work out the details.
Thank you.sir, I saw the @Michal_Adamaszek’s solution yesterday, but my problem is not similar to (1+x/(1+x)), my problem is similar to (1+x/(1+y)). so in cvx ,how to use cvx function to express or substitute (1+x/(1+y)), I have no idea.
For example, (1+p6k/(N0+p1k+p2k+p3k+p4k+p5k)) be expressing by (1+p6k.*inv_pos(N0+p1k+p2k+p3k+p4k+p5k)) is incorrect.
Sorry, I misread the problem when I formulated my previous answer. I am back to claiming this problem is non-(jointly) convex (unless I just made a mistake). The objective function Hessian can be indefinite.
If you believe I am incorrect in this assessment, prove it.
Sorry, the problem is non-convex by proved.