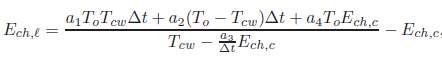You’re right. The full code is:
m = 3; % Number of agents;
M = 144; % Number of time slots;
Dt = 600; % Width of the time slot [s];
a1=0.0109;
a2=20.22;
a3=3.8;
a4=0.9327;
Echmax=0.05*Dt;
Tcw=283;
To=295;
S0 = 750; % Storage initial condition [MJ];
Smax = 1425; % Storage max capacity [MJ];
Smin = 75; % Storage max capacity [MJ];
smax = 33; % Storage max flow [MJ];
smin = -smax; % Storage min flow [MJ];
Losses = 0.99; % Percent of losses per hour;
ratio = 10; % alpha = mean(beta)/ratio;
usebeta = 1; % 1 = use beta, 0 = do not;
c = 0.0037; % Proximal coefficient;
cTz = 0.01; % Penalization term on Temperatures;
cs = 0.0001; % Penalization term on Storage;
deltabar = 1e-6; % Dual ascent gain;
gamma = 0.1; % Dual ascent vanishing parameter;
epsilonRo = 1e-3; % Relative convergence tollerance outer layer;
epsilonAo = 1e-3; % Absolute convergence tollerance outer layer;
epsilonRi = 1e-1; % Relative convergence tollerance inner layer;
epsilonAi = 1e-1; % Absolute convergence tollerance inner layer;
%------------- Optimization -----------------------------------------------
cvx_begin
cvx_quiet(true)
%-------- Optimization variables ------------------------------------------
variable h(M,1); % Epigraphic reformulation;
variable Tz(M+1,m); % Temperatures;
variable s(M,m); % Storage flow;
dual variable y0; % To check tight;
dual variable y1; % Optimal multipliers;
dual variable y2; % Optimal multipliers;
dual variable y3; % Optimal multipliers;
cvx_precision high % May cause failure
Penalization = 0; % Inizialization
for i = 1:m % For each building
% Stationary solution for the building state;
x0(:,i) = inv(eye(Building.Parameters.ns)-(Building.Model.Ax))*...
(Building.Model.Bx*Tz(:,i)+Building.Model.Wx*Disturbances.Mean);
% Energy required for cooling;
Ec(:,i) = Building.Model.As*x0(:,i) +...
+ Building.Model.Bs*Tz(:,i) +...
+ Building.Model.Ws*Disturbances.Mean +...
+ Disturbances.Internal +...
+ Disturbances.People + ...
+ Disturbances.Radiation;
% Energy required to the chiller;
Ech(:,i) = Ec(:,i) - s(:,i);
% Electricity
El(:,i)=(a1*To*Tcw*Dt+a2*(To-Tcw)*Dt+a4*To*Ech(:,i)).*pow_p(Tcw-a3*Ech(:,i)/Dt,-1)-Ech(:,i);
% Penalization
Penalization = Penalization + ...
+ cTz*pow_pos(norm(Tz(:,i)-(273+23),2),2) + ...
+ cs*pow_pos(norm(s(:,i),2),2);
% "pow_pos(norm(x,2),2)" is better than "traspose(x)*x"
end
% Storage Energy content
S = Storage.Model.A*S0 + Storage.Model.B*sum(s,2);
% -------- Problem formulation ---------------------------------------------
minimize transpose(beta + alpha*h)*h + Penalization
subject to
for i = 1:m
% Comfort constraints
Tz(:,i) <= Building.Constraints.Tzmax;
Tz(:,i) >= Building.Constraints.Tzmin;
% Technical limits
Ech(:,i) <= Chiller{i}.Constraints.Echmax;
end
% Closure contraint - initial condition
Tz(1,1:i) == Tz(end,1:i);
Tz(1,1:i) == ones(1,m)*(273+24);
% Do not heat
Ec >= 0;
Ech >= 0;
% Absorbed Electricity
y0:sum(El,2) <= h;
% Storage Constraints
s <= Storage.Constraints.smax/3;
s >= Storage.Constraints.smin/3;
y1:S >= Storage.Constraints.Smin;
y2:S <= Storage.Constraints.Smax;
y3:S(end) >= S0;
cvx_end
%-------- Solution check --------------------------------------------------
% Tightness
if any(y0 == 0)
disp('Error: solution is not tight');
end
% Complementary slackness
A = [- Storage.Model.B
+ Storage.Model.B
- Storage.Model.B(end,:)];
b = [- Storage.Constraints.Smin + Storage.Model.A*S0
+ Storage.Constraints.Smax - Storage.Model.A*S0
+(Storage.Model.A(end)-1)*S0];
if any( [y1.*(-A(1:M,:)*sum(s,2) + b(1:M));
y2.*(-A(M+1:2*M,:)*sum(s,2) + b(M+1:2*M));
y3.*(-A(end,:)*sum(s,2) + b(end))]>=1e-5)
disp('Error: solution is not optimal');
end
% Results --- display -----------------------------------------------------
Total_Cost = transpose(beta + alpha*h)*h + Penalization;
Electricity = transpose(beta + alpha*h)*h;
LinearCost = transpose(beta)*h;
QuadraticCost = transpose(alpha*h)*h;
Penalization;
TempPenal = 0;
sPenal = 0;
for i=1:3
TempPenal = TempPenal+cTz*(Tz(:,i)-(273+23))'*(Tz(:,i)-(273+23));
sPenal = sPenal + cs*transpose(s(:,i))*s(:,i);
end
disp(['Total Cost J = ',num2str(Total_Cost)])
disp(['Electricity = ',num2str(Electricity)])
disp(['Linear share = ',num2str(LinearCost)])
disp(['Quadratic share = ',num2str(QuadraticCost)])
disp(['Penalization = ',num2str(Penalization)])
disp(['Temperature share = ',num2str(TempPenal)])
disp(['Exchange share = ',num2str(sPenal)])
As far as the convexity of that expression is concerned, I was said by my supervisor that it’s convex and it sould be proved by this picture
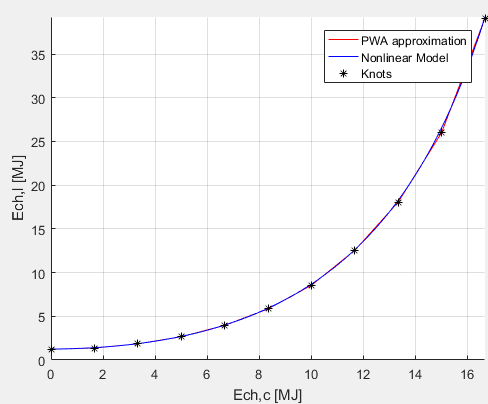
What’s wrong in my code?
Thanks in advance for each hint I’m gonna be given,
Paolo