Hello, I am trying to solve an optimization problem as shown below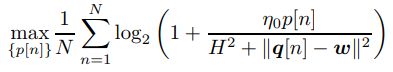
subject to the following constraints:
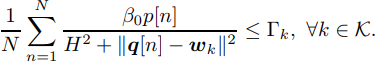
![]()
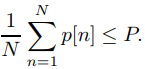
where p[n] is power being transferred in a cognitive wireless communications network, and gamma outlines a predetermined interference limit which needs to be minimized. I have written the following code in CVX to model the problem above:
K = 2; %Number of primary users
T = 200; %Mission time period
f_s = 1; %sample frequency
N = T/f_s; %Number of timesteps
delta_t = 1/f_s; %sample period
H = 100; %Altitude
b_0 = 10^-3; %Beta naught channel power gain
q_i = [-1000 1000]; %initial UAV pos
q_f = [1000 -1000]; %final UAV pos
sigma_squared = 10^-8; %Sigma squared SNR level
q_n = zeros(N,2); %vector space for optimized trajectory
qj_n = zeros(N,2); %Previous iteration trajectory
for i = 1:N %designing straight line trajectory
qj_n(i,1) = ((2000/(N-1))*(i-1))-1000;
qj_n(i,2) = 1000 - ((2000/(N-1))*(i-1));
end
qj_n(N,1) = q_f(1,1);
qj_n(N,2) = q_f(1,2);
p_ave = 0; %average optimized power
w_sr = [0 0]; %Secondary user position
P = 1; % power threshold
gamma_k = 10^-12; % interference threshold
w_k = [-500 500; 500 -500]; %position of primary users
p_n = zeros(N,1); %vector for optimized power value at p(i)
cvx_clear;
fprintf('Optimization program has started \n');
[p_n, p_ave] = p_opt(K, N, H, b_0, sigma_squared, qj_n, w_sr, P, gamma_k, w_k);
fprintf('The optimized power is %d\n', p_ave);
function [p_optimized, p_rate] = p_opt(K, N, H, b_0, sigma_squared, qj_n, w_sr, P, gamma_k, w_k)
cvx_begin;
n_0 = b_0/sigma_squared;
p_optimized = cvx(zeros(N,1)); %vector for optimized power value at p(i)
int_k = cvx(zeros(K,1)); %interference to each primary user at position q(i)
p_sum = 0;
variable x(N,1)
for i=1:N %finding sum of optimized power
p_sum = p_sum + (-rel_entr(1, 1 + ((n_0 * x(i,1))/(H^2 + sum_square(qj_n(i,:) - w_sr)))))/log(2);
p_optimized(i,1) = x(i,1);
end
p_rate = p_sum/N;
maximize (p_rate);
subject to
for i=1:N %power cannot be negative
x(i,1) >= 0;
% x(i) <= 2;
end
(sum (x))/N <= P; %average power cannot be above the threshold
for i=1: K %interference constraint
int_p = 0;
for j=1:N
int_p = int_p + ((b_0*x(j,1))/(H^2 + sum_square(qj_n(j,:)-w_k(i,:))));
end
int_k(i,1) = int_p/N;
int_k(i,1) <= gamma_k;
end
cvx_end;
end
When running this CVX ignores the interference constraint (gives solved interference of 0.35x10^8 when it needs to be below 10^12) and results in an inaccurate/solved status. It would seem intuitive that if all values of power were simply scaled down to a lower value then you could satisfy the interference constraint, but CVX does not seem to want to do this.
Any advice on why this may be happening would be appreciated. Thank you.