Hi, I’m a student and this is my first approach to optimization and obviously the same for cvx . I trying to develop a guidance control algorithm and it works if I consider a simple optimization problem as follow(it works well on 4°order system built on the same philosophy but i will use 1° order system for to explain my problem in a simple way ):
I rewrite my system in such a way to eliminate the dependence to x(k)
% x(2:k+1)=Fxo+Hu =
% x[2:k+1] =[A … A^k]'x0 + [ A^0B 0 … 0 ]
% %%%%%%%%%%%%%[ A^1*B B 0 0 ]U_vett(1:K)
% %%%%%%%%%%%%%[ … … B 0 ]
%%%%%%%%%%%%%%[ A^kB A^(k-1)B A^(k-2)B A^(k-n)B ]
% with A=1 B=1
clear all
clc
N=3;
%x(2:k+1)=Fxo+Hu
F=[1;1;1];
H=[1 0 0;1 1 0;1 1 1];
cvx_begin
variables u(N) v(N)
minimize( u’*u)
subject to
v==Fv(1)+Hu*0.1;
-10<=u<=10
v(1)==0;
v(N)==1;
cvx_end
figure(1)
hold on
plot(v,‘b’)
plot(u,‘r’)
BUT if I consider the optimization problem as follow :
. 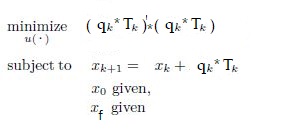
It doesn’t work and the causes is q.T(element-wise multiplication) and i don’t understand why. q.T is a column vector as u in the previous example. The . is supported in CVX as written on reference guide–>Arithmetic operators
the code is the following:
clear all
clc
N=3;
cvx_begin
variables q(N) T(N) v(N)
minimize( (q.T)’(q.*T)+v’*v)
subject to
v==[1;1;1]*v(1)+[1 0 0;1 1 0;1 1 1]*q.T0.1;
-1<=T<=1
-1<=q<=1
v(1)==0;
v(N)==10;
cvx_end
%Error using .* (line 262)
%Disciplined convex programming error:
%Invalid quadratic form(s): not a square.
I had tried to create a function inside CVX but don’t work.
I hope that someone could help me. I would be very very gratefull