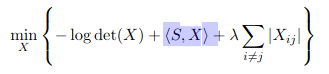I have a minimization objective like this:
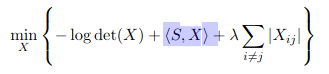
In my code I am trying to represent it as:
cvx_begin
variable X(size(A));
idx = eye(size(A));
Y = (1-idx).*X;
minimize ( -log_det(X) + S * X + lambda * Y );
cvx_end
I am getting this error:
Your objective function is not a scalar.
A is a random matrix the same size as S.
Can you all please suggest what I am doing wrong? Thanks!
I suggest you read whatever paper or book you are getting this from more carefully and try to understand the material in it. Obviously, a non-scalar matrix objective function makes no sense, which would be apparent if you thought about it.
<S,X> means trace(S'*X), which is an affine function which can be directly entered into CVX. It also happens to equal sum(sum(S.*X)), which could be alternatively used.
S*X is a matrix, and therefore, per the rules of MATLAB, so is the objective function. Hence the CVX error ,message.
I don’t believe Y is correct. I believe
Y = trace((1-idx)*abs(X))
or
Y = sum(sum((1-idx).*abs(X))) would do the trick.
Actually it’s an assignment question.
I defined X as:
variable X(size(A));
Well, it’s better for you to understand your assignments, not blindly do things which don’t make any sense. Please ask your Prof to give me an A.